Introduction #
Extreme events #
- financial (and claims) data has often leptokurtic severity (more peaked - heavy tailed - than normal)
- reasons include heteroscedasticity (stochastic volatility)
- almost by definition, extreme events happen with low frequency
- but extreme events are the ones leading to financial distress, possibly ruin
- accurate fitting is crucial for capital and risk management (risk based capital, reinsurance, ART such as securitisation via CAT bonds)
- fitting presents specific issues:
- there is little data to work from
- when fitting a whole distribution, the big bulk of the data (around the mode) overpowers observations in the tails in the optimisation routine (MLE), leading to poor fit in the tail
- sometimes (in fact, almost always) a good distribution for the far tail is different from that for the more common outcomes.
Framework #
- Consider iid random variables
- We denote the order statistics
- Specifically, we may be interested in
Motivating example (Paul Embrechts, Resnick, and Samorodnitsky 1999) #
Consider the following situation:
- Let
- We have
- The maximum observed was 50. How likely is it if the model is correct? What if the maximum had been 100?
The probability that the maximum
A limiting argument #
We now perform the following calculations:
General result for
We can easily generalise the previous result to any
This means that for large
Indeed, this works well for our example, especially in the tail:
Questions #
- This is nice, but not all random variables are exponential.
- Can we generalise such a limiting approach to any df?
Yes!
- Can we find norming constants (such as
That is, how do we find
We can! (there are only three cases to consider), but we won’t discuss that here (see, e.g., P. Embrechts, Klüppelberg, and Mikosch 1997 for the proofs)
Generalised Extreme Value distribution #
The GEV distribution #
Parallel with CLT #
The theoretical results of the previous section lead to an extreme value complement or homologue, for the tails, of the CLT approximation (which works only around the middle of the distribution).
- In the exponential example, the “normalised” maximum
- This generalises to any distribution for
Extreme Value Distributions #
The Gumbel distribution
The last one relates to the heavy tailed distributions (typically with moments existing only up to a certain order, infinite afterwards),
and is the most relevant to actuarial applications.
Three cases #

(Unit 4, Page 4, IoA 2020) Note
GenEV <- function(x, alpha, beta, gamma) {
1/beta * (1 + gamma * (x - alpha)/beta)^(-(1 + 1/gamma)) *
exp(-((1 + gamma * (x - alpha)/beta)^(-1/gamma)))
}
par(mfrow = c(1, 3), oma = c(0, 0, 3, 0))
plot(-4000:2000/1000, GenEV(-4000:2000/1000, 0, 1, -0.5), main = "Density with gamma=-0.5 (Weibull)",
xlim = c(-4, 4), xlab = "", ylab = "", cex = 1)
plot(-4000:4000/1000, GenEV(-4000:4000/1000, 0, 1, 1e-05), main = "Density of GEV with gamma=0 (Gumbel)",
xlim = c(-4, 4), xlab = "", ylab = "", cex = 1)
plot(-2000:4000/1000, GenEV(-2000:4000/1000, 0, 1, 0.5), main = "Density of GEV with gamma=0.5 (Fréchet)",
xlim = c(-4, 4), xlab = "", ylab = "", cex = 1)
mtext("Density of GEV with mu=0, sigma=1, and various values of gamma",
outer = TRUE, cex = 1.5)

Estimation: Block Maxima #
- The EVD is a distribution of maxima
- To fit it we need a sample of maxima
- To achieve this, the data is transformed into block maxima
- assume we have
- consider blocks of length
- the block maxima are the equal to the maximum observation within a block
- we have then a sample size of
- assume we have
- The block maxima are then fitted to the EVD
- The larger the block size, the closer to the asymptotic distribution we get, but the less data we have: conflicting requirements
- In R, this can be done efficiently with the function
fevdof the packageextRemes(Gilleland and Katz 2016)
Case study - data #
Data sets #
We consider three simulated data sets with
| month | beta | gamm | logg |
|---|---|---|---|
| 61 | 12862.84 | 33493.02 | 18773.47 |
| 62 | 408.64 | 6070.20 | 7564.21 |
| 63 | 2404.87 | 26093.36 | 5083.10 |
| 64 | 4753.73 | 3773.61 | 2070.88 |
| 65 | 594.57 | 3885.25 | 43601.62 |
| 66 | 16805.64 | 6881.97 | 6163.90 |
| 67 | 4335.52 | 5163.38 | 8158.35 |
| 68 | 5575.15 | 24401.76 | 19172.13 |
claims <- as_tibble(read_excel("simulated-claims.xlsx"))
summary(claims$beta)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0 2102 7585 10078 16532 33287
summary(claims$gamm)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 6.12 3566.46 7668.73 10107.70 14070.25 90712.14
summary(claims$logg)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 432.7 4611.7 7374.7 9931.9 12124.2 157377.1
plotdist(claims$beta)
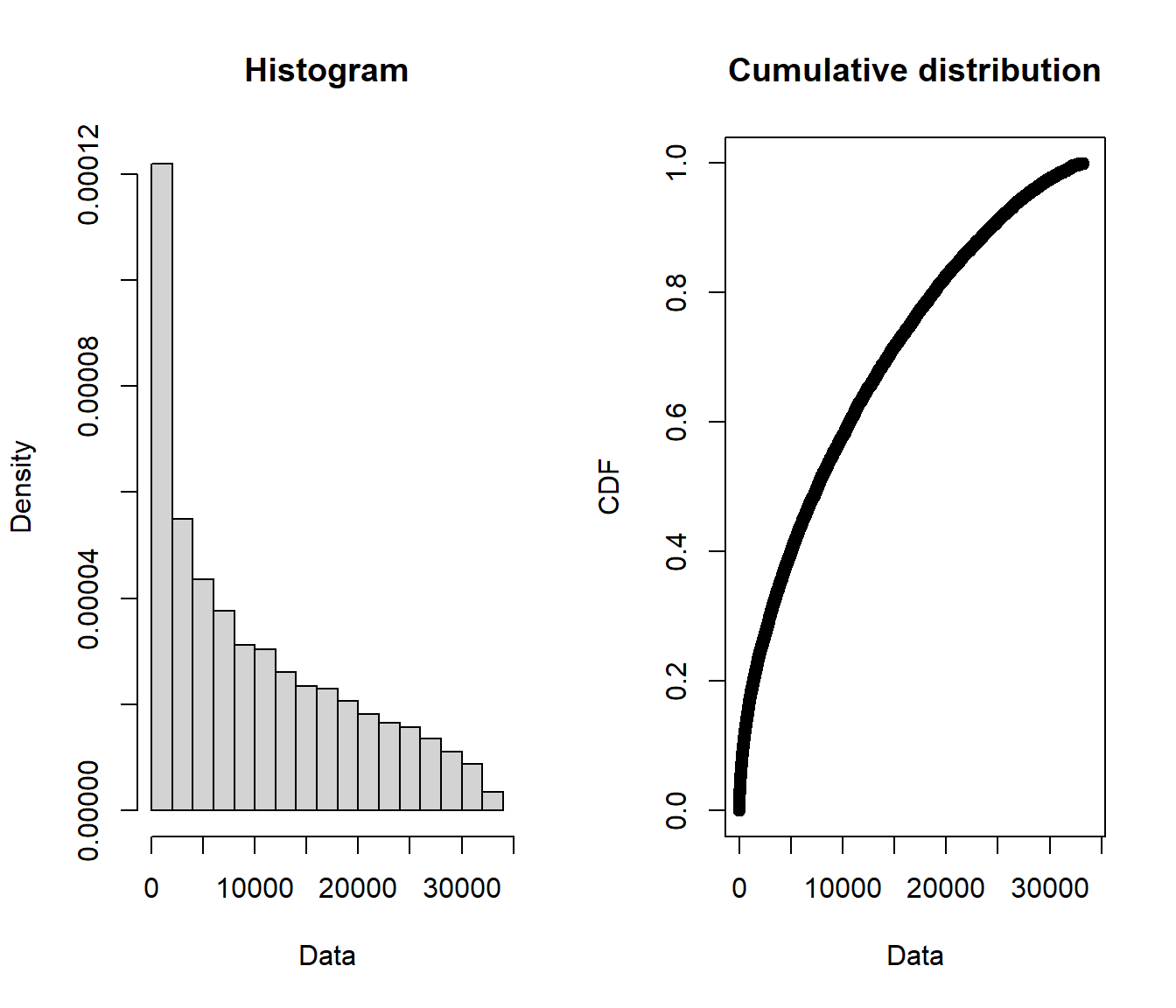
plotdist(claims$gamm)
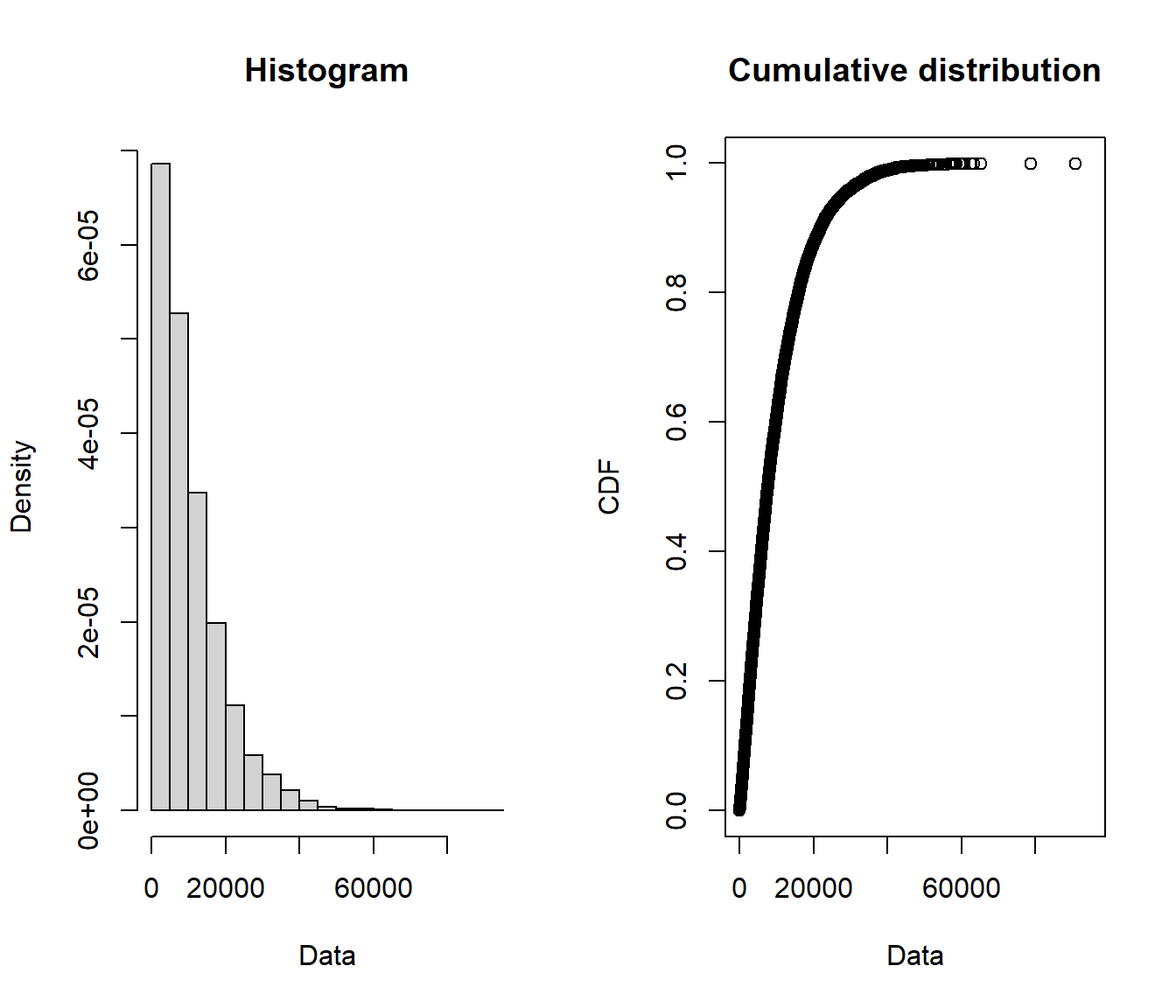
plotdist(claims$logg)
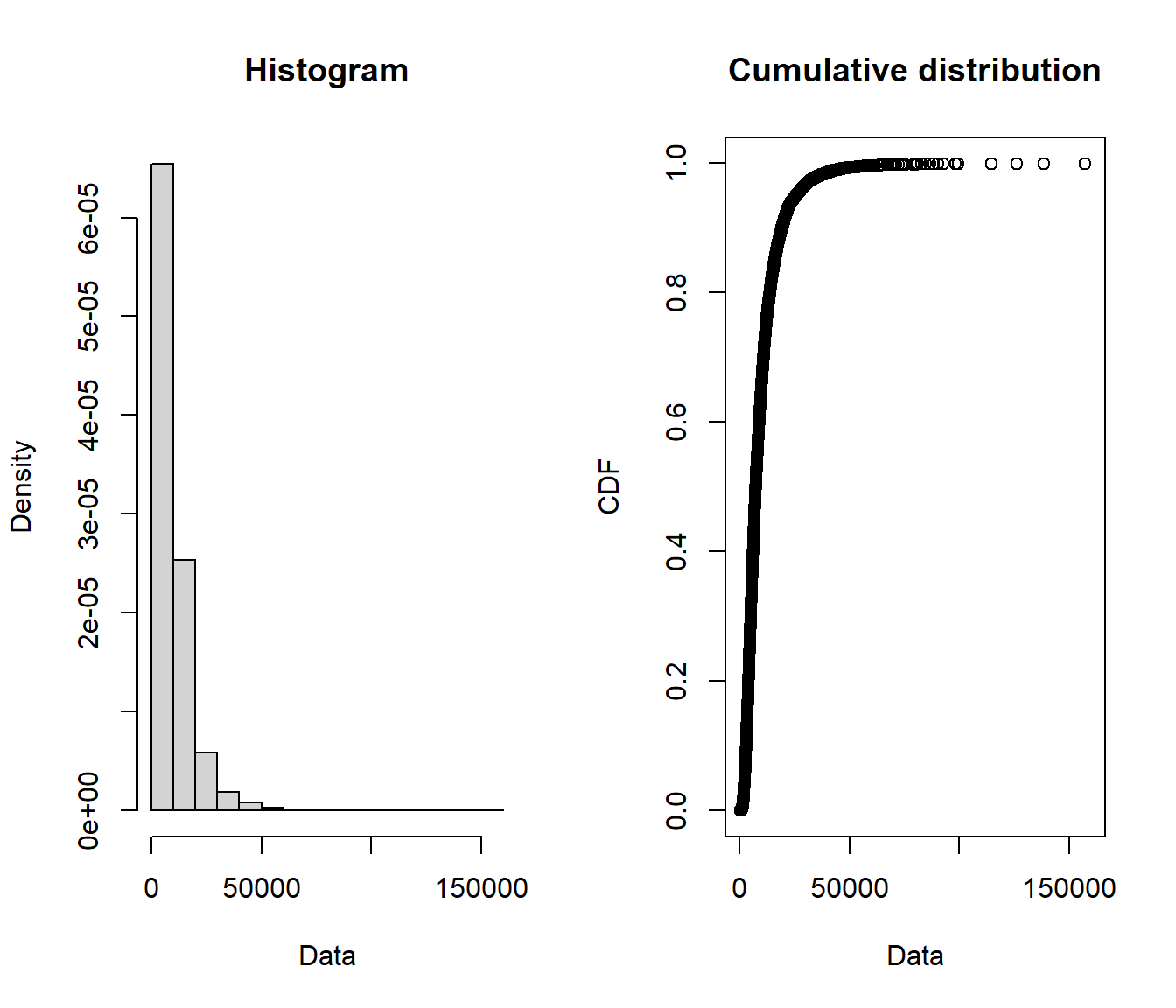
Block maxima #
Creating block maxima
# block maxima index
claims$block <- (claims$month - 1)%/%12 + 1
# %/% gives the integer part of the result of the division
blockmax <- tibble(betablock = aggregate(beta ~ block, claims,
max)$beta, gammblock = aggregate(gamm ~ block, claims, max)$gamm,
loggblock = aggregate(logg ~ block, claims, max)$logg)
# have a look at what the aggregate function does
We now have a sample of
What do these look like in comparison with the original data?
claims <- as_tibble(read_excel("simulated-claims.xlsx"))
summary(blockmax$betablock)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 11376 23803 27155 26606 30035 33287
summary(blockmax$gammblock)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 9521 21036 27278 28479 34299 90712
summary(blockmax$loggblock)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 9326 18618 24590 28587 33259 157377
plotdist(blockmax$betablock)
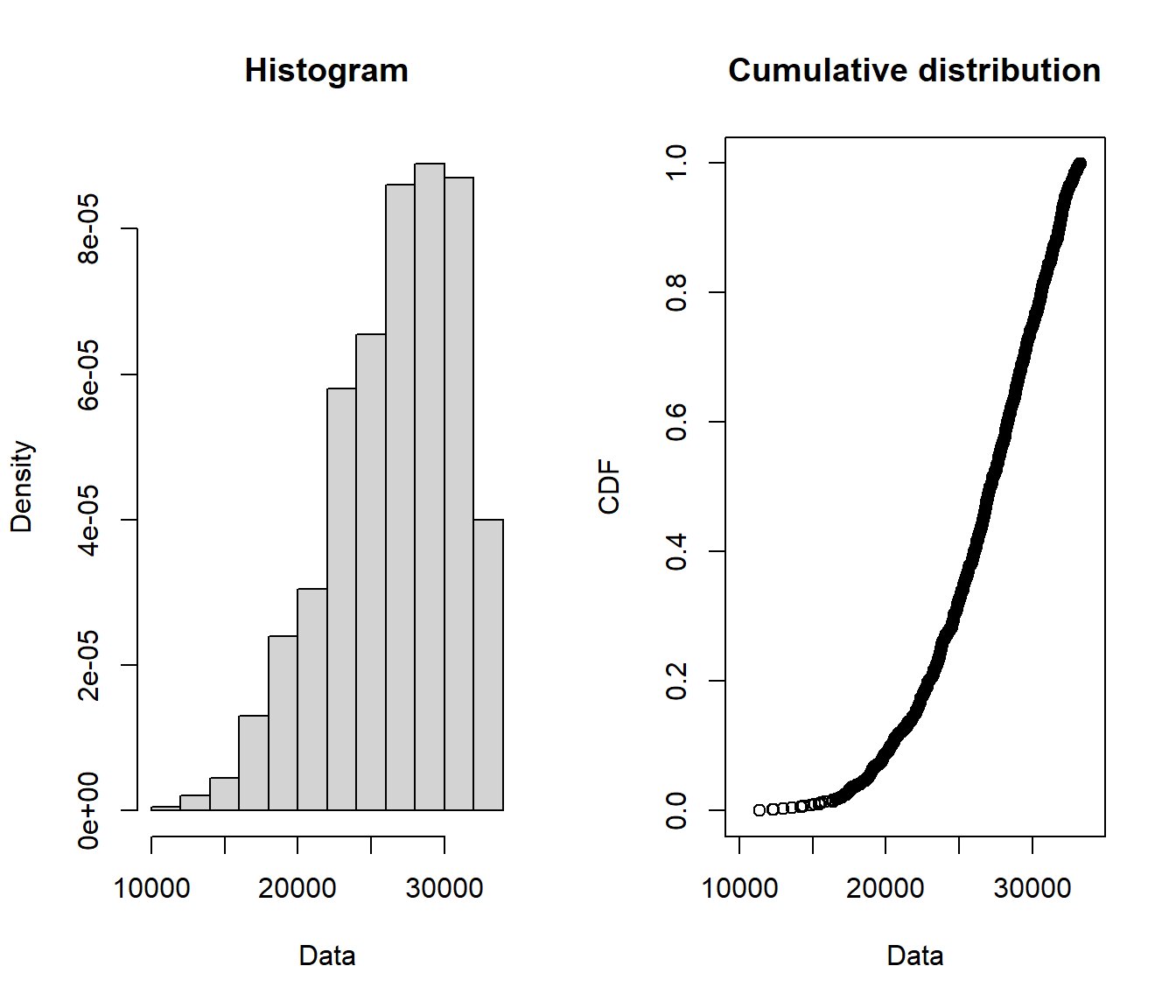
plotdist(blockmax$gammblock)

plotdist(blockmax$loggblock)
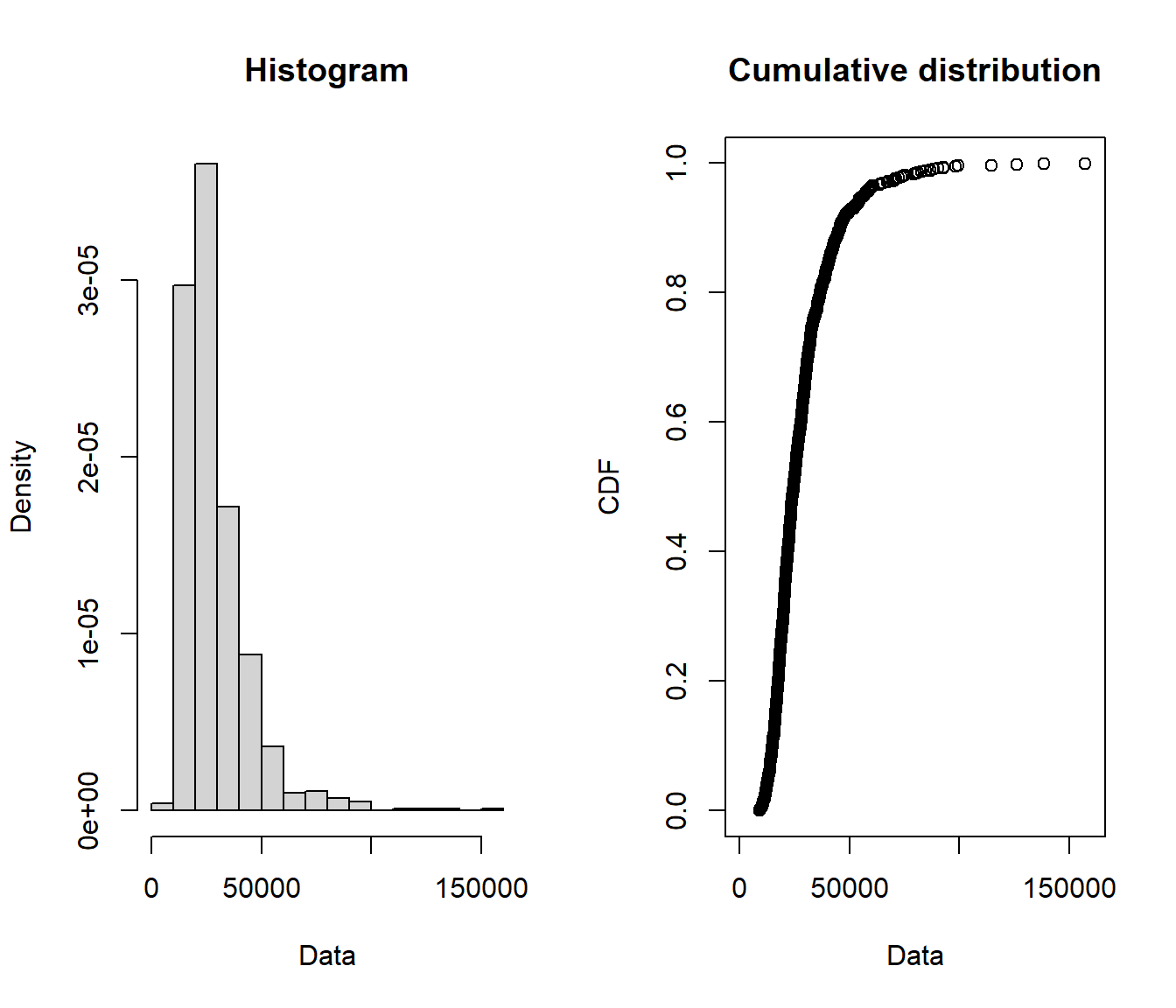
par(mfrow = c(1, 2))
plot(density(claims$beta), main = "Density of the beta claims",
xlab = "Claim amounts ($)", xlim = c(0, max(claims$beta)))
plot(density(blockmax$betablock), main = "Density of the beta block maxima",
xlab = "Maximums over consecutive periods of 12 months ($)",
xlim = c(0, max(claims$beta)))
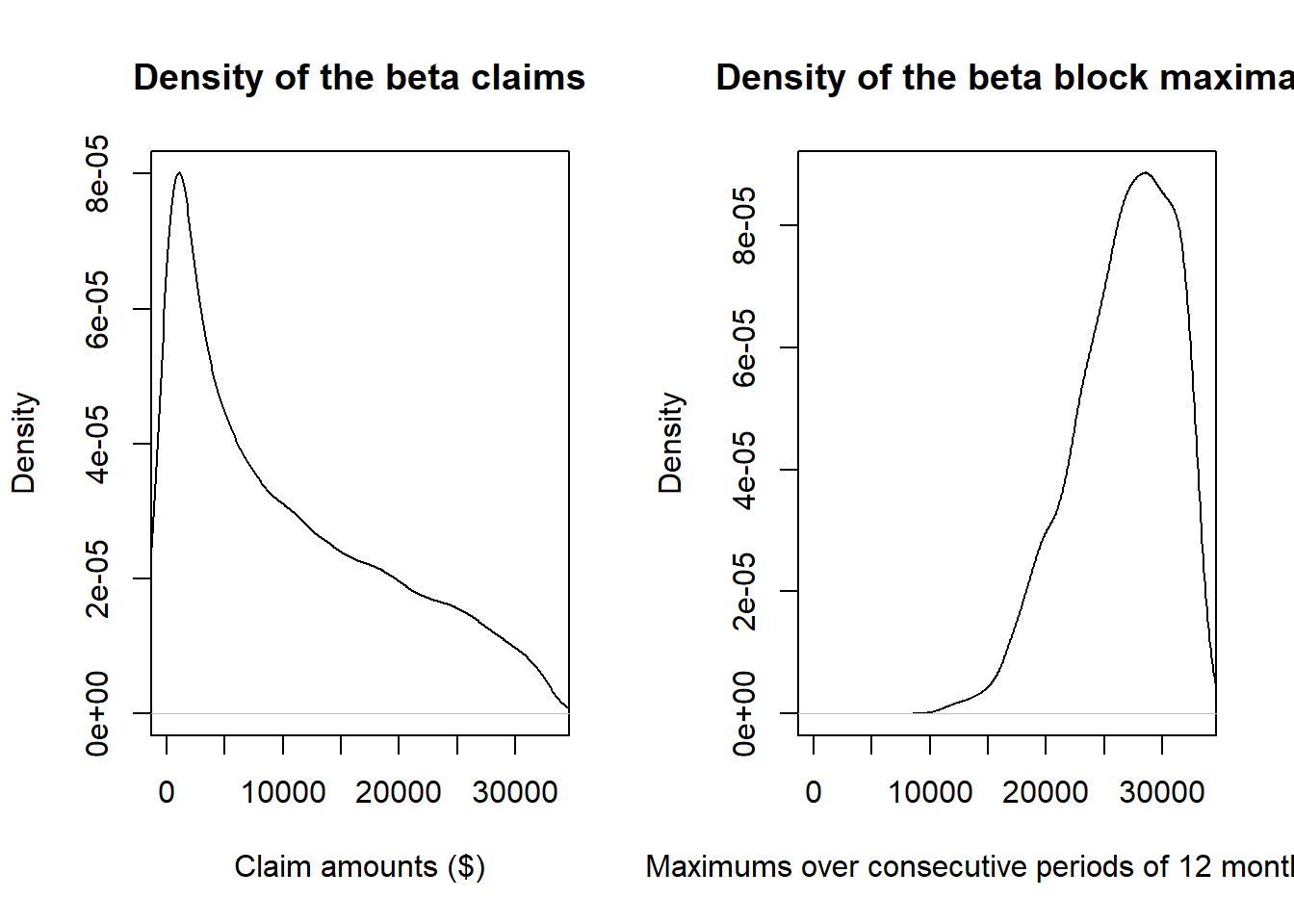
par(mfrow = c(1, 2))
plot(density(claims$gamm), main = "Density of the gammormal claims",
xlab = "Claim amounts ($)", xlim = c(0, max(claims$gamm)))
plot(density(blockmax$gammblock), main = "Density of the gammormal block maxima",
xlab = "Maximums over consecutive periods of 12 months ($)",
xlim = c(0, max(claims$gamm)))
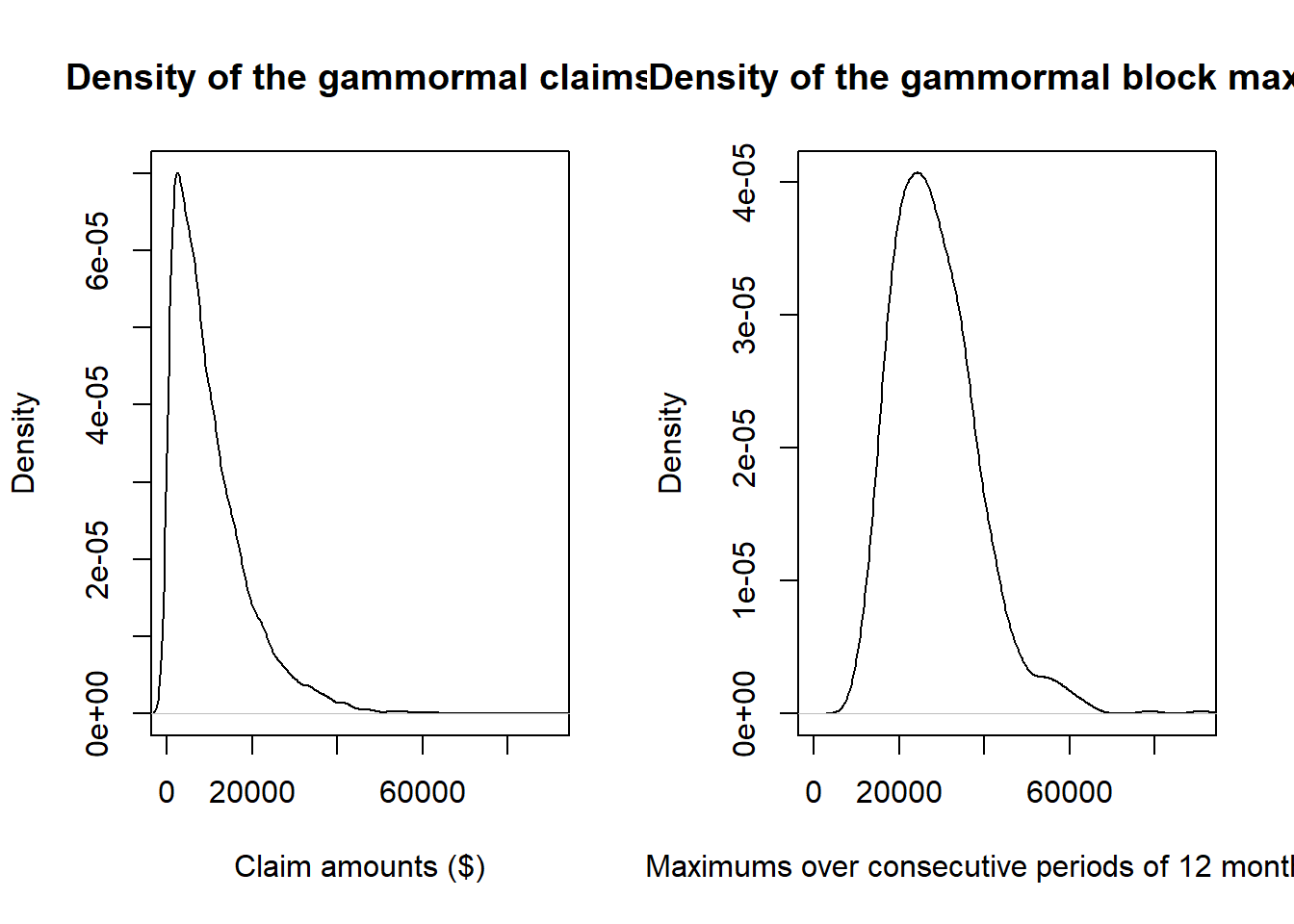
par(mfrow = c(1, 2))
plot(density(claims$logg), main = "Density of the log-gamma claims",
xlab = "Claim amounts ($)", xlim = c(0, max(claims$logg)))
plot(density(blockmax$loggblock), main = "Density of the log-gamma block maxima",
xlab = "Maximums over consecutive periods of 12 months ($)",
xlim = c(0, max(claims$logg)))
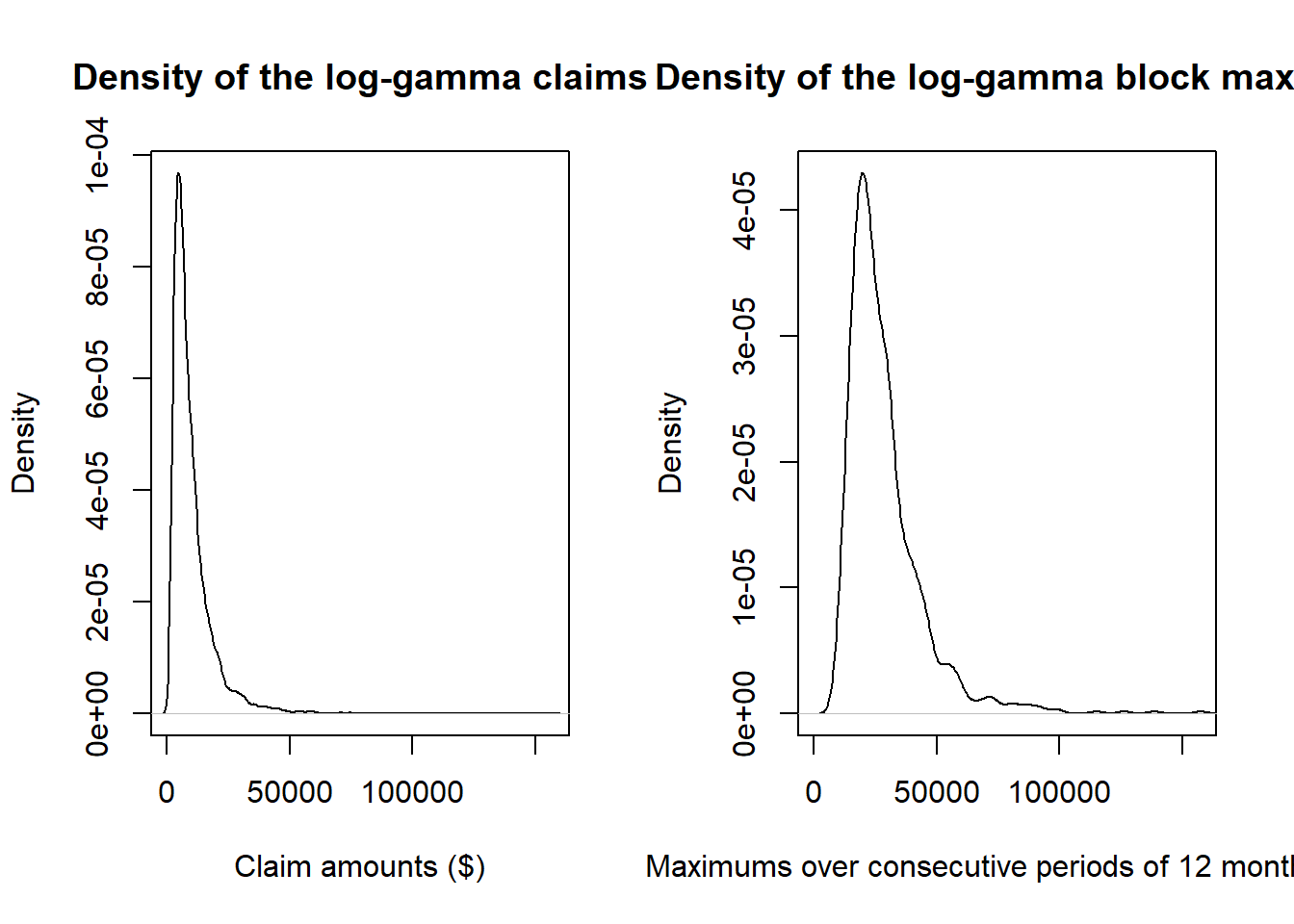
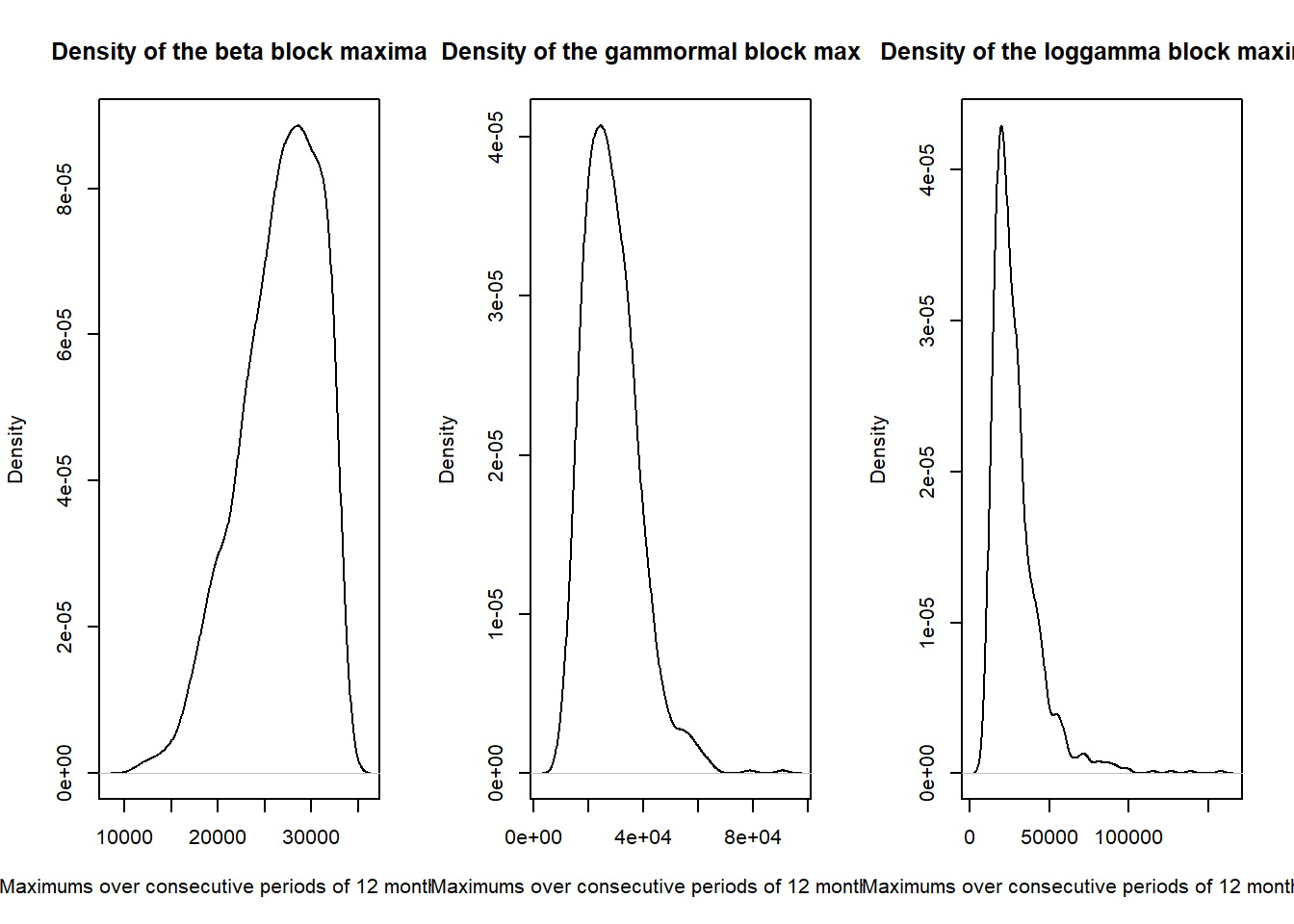
par(mfrow = c(1, 3))
plot(density(blockmax$betablock), main = "Density of the beta block maxima",
xlab = "Maximums over consecutive periods of 12 months ($)")
plot(density(blockmax$gammblock), main = "Density of the gammormal block maxima",
xlab = "Maximums over consecutive periods of 12 months ($)")
plot(density(blockmax$loggblock), main = "Density of the loggamma block maxima",
xlab = "Maximums over consecutive periods of 12 months ($)")
Case study - fitting #
Fitting results #
For example for the logg BM we use the following code:
fit.logg <- fevd(blockmax$loggblock)will perform the fitfit.loggwill display the results of the fittingplot(fit.logg)will plot goodness of fit graphical analysisplot(fit.logg,"trace")will plot the likelihood function around the chosen parameters
More details can be found in Gilleland and Katz (2016).
Results (MLE with standard errors in parentheses) are
| location |
scale |
shape |
|
|---|---|---|---|
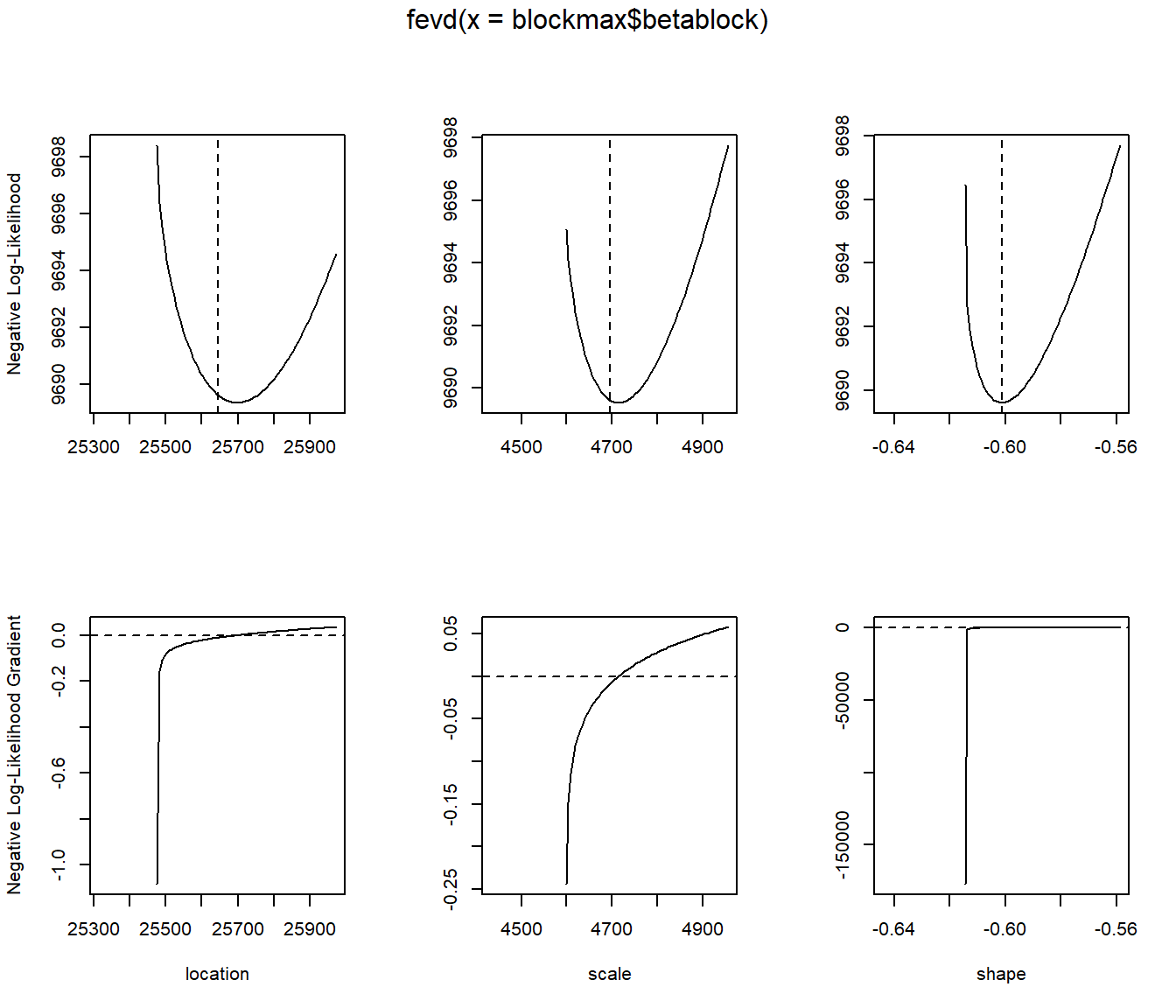
| beta | 25644.93 (163.26) | 4695.76 (130.07) | -0.6012 (0.0212) |
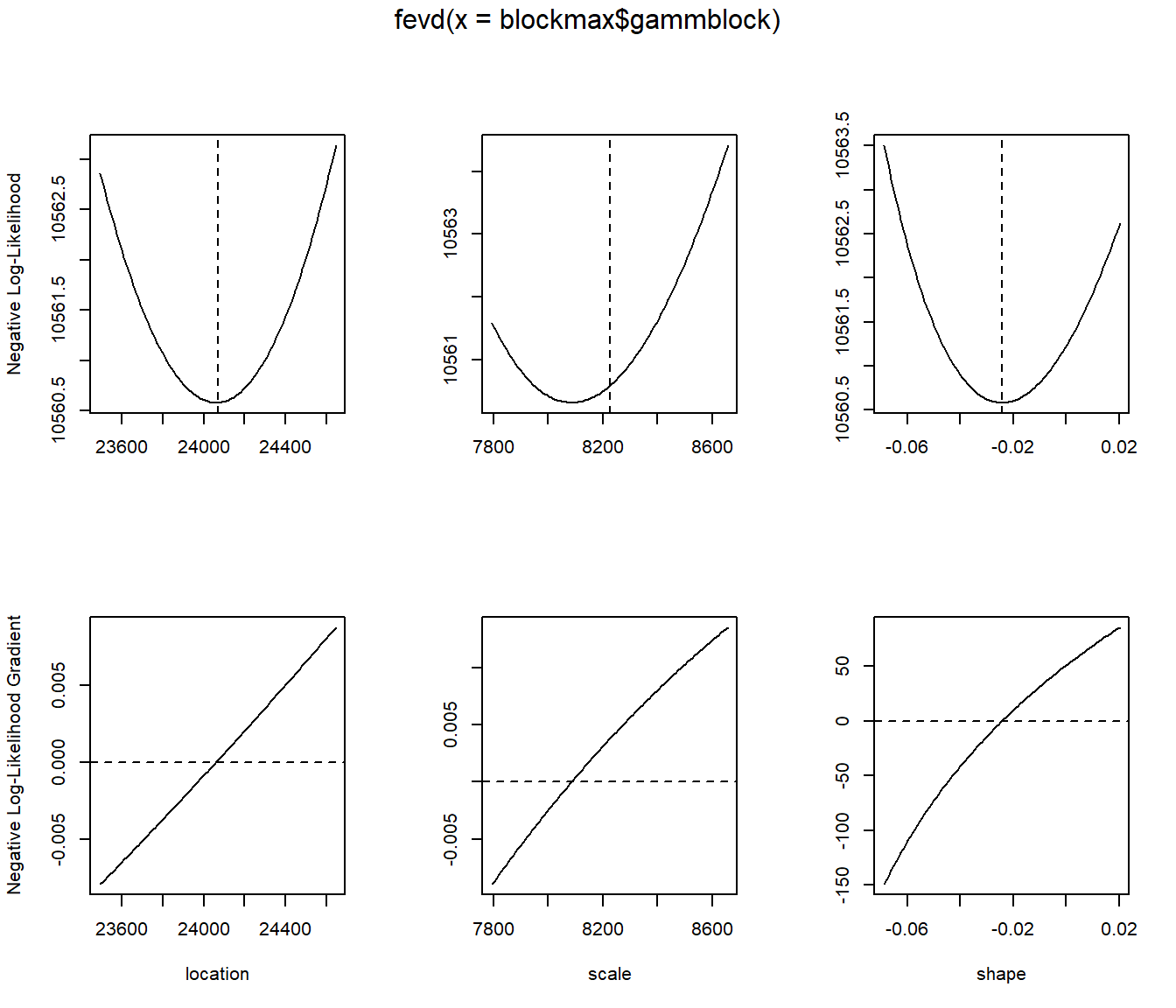
| gamma | 24069.68 (288.51) | 8225.98 (215.80) | -0.0243 (0.0222) |
| loggamma | 21466.22 (305.26) | 8496.86 (251.97) | 0.2299 (0.0278) |
Note:
- These correspond to the three distinct cases introduced before as expected (look at the sign of
- Whether
fit.beta <- fevd(blockmax$betablock)
fit.beta
...
## Estimated parameters:
## location scale shape
## 25644.9318770 4695.7556362 -0.6011579
##
## Standard Error Estimates:
## location scale shape
## 163.26448100 130.06953700 0.02120487
##
## Estimated parameter covariance matrix.
## location scale shape
## location 26655.290757 -8463.804100 -1.2827274803
## scale -8463.804100 16918.084456 -1.7746705470
## shape -1.282727 -1.774671 0.0004496465
##
## AIC = 19385.23
##
## BIC = 19399.96
...
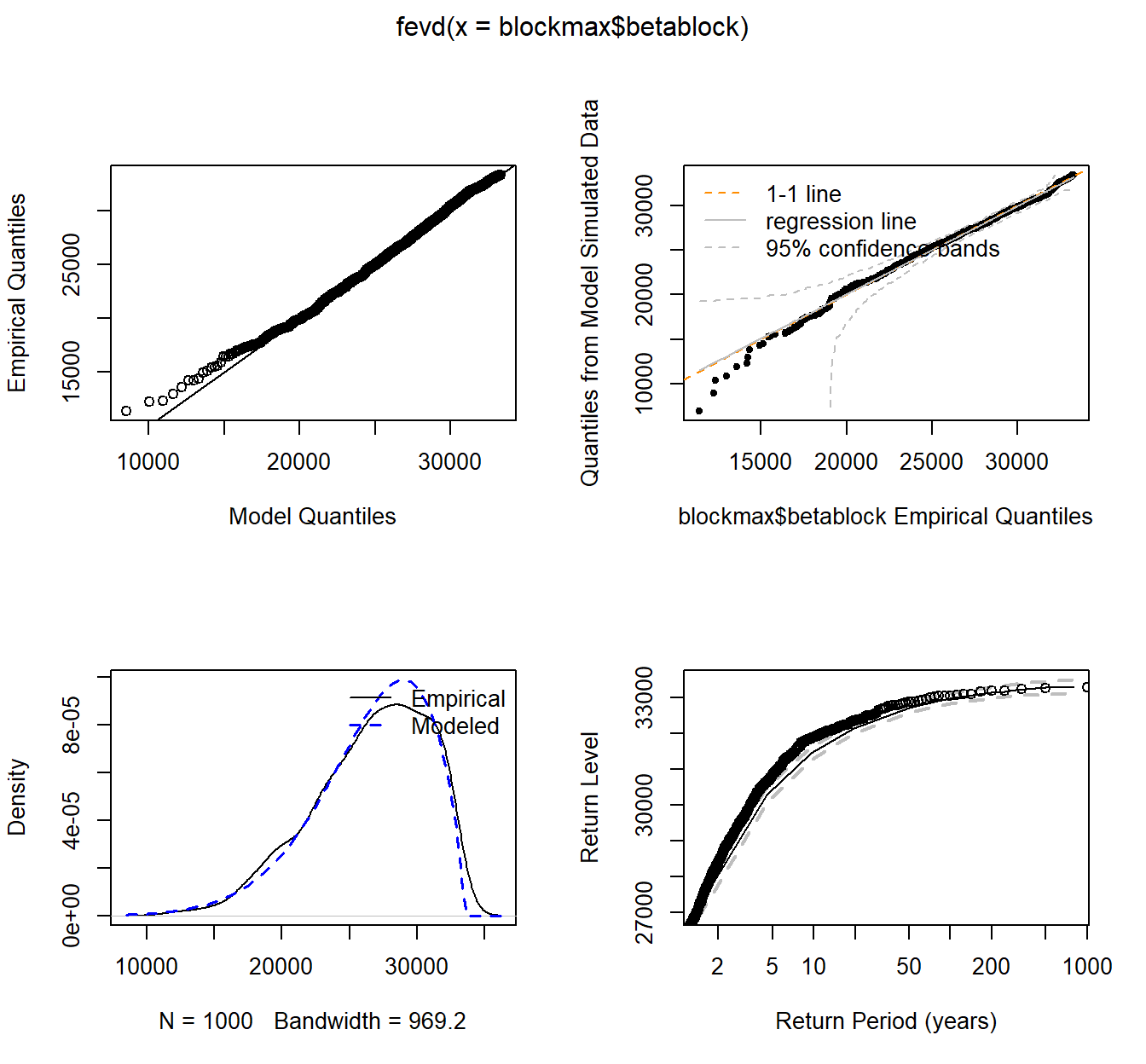
plot(fit.beta)
plot(fit.beta, "trace")
fit.gamm <- fevd(blockmax$gammblock)
fit.gamm
...
## Estimated parameters:
## location scale shape
## 2.406968e+04 8.225984e+03 -2.428561e-02
##
## Standard Error Estimates:
## location scale shape
## 288.51126800 215.80132748 0.02220903
##
## Estimated parameter covariance matrix.
## location scale shape
## location 83238.751764 21650.966827 -2.0732936569
## scale 21650.966827 46570.212942 -1.4944274045
## shape -2.073294 -1.494427 0.0004932409
##
## AIC = 21127.17
##
## BIC = 21141.89
...
plot(fit.gamm)

plot(fit.gamm, "trace")
fit.logg <- fevd(blockmax$loggblock)
fit.logg
...
## Estimated parameters:
## location scale shape
## 21466.224267 8496.863050 0.229869
##
## Standard Error Estimates:
## location scale shape
## 305.26319626 251.96813338 0.02779193
##
## Estimated parameter covariance matrix.
## location scale shape
## location 93185.618989 45516.589594 -2.5704729001
## scale 45516.589594 63487.940241 -0.5065090268
## shape -2.570473 -0.506509 0.0007723913
##
## AIC = 21491.68
##
## BIC = 21506.4
...
plot(fit.logg)
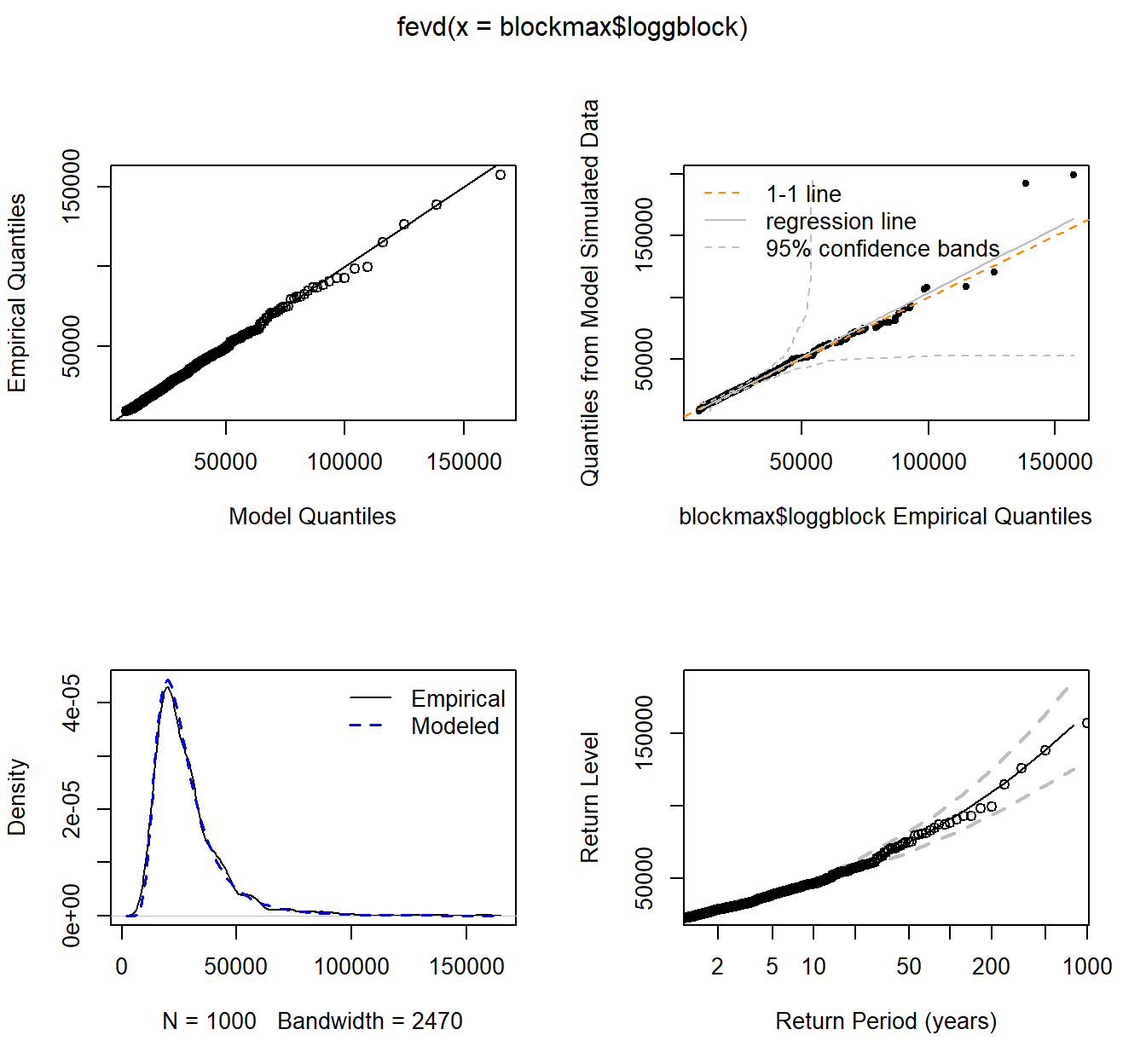
plot(fit.logg, "trace")
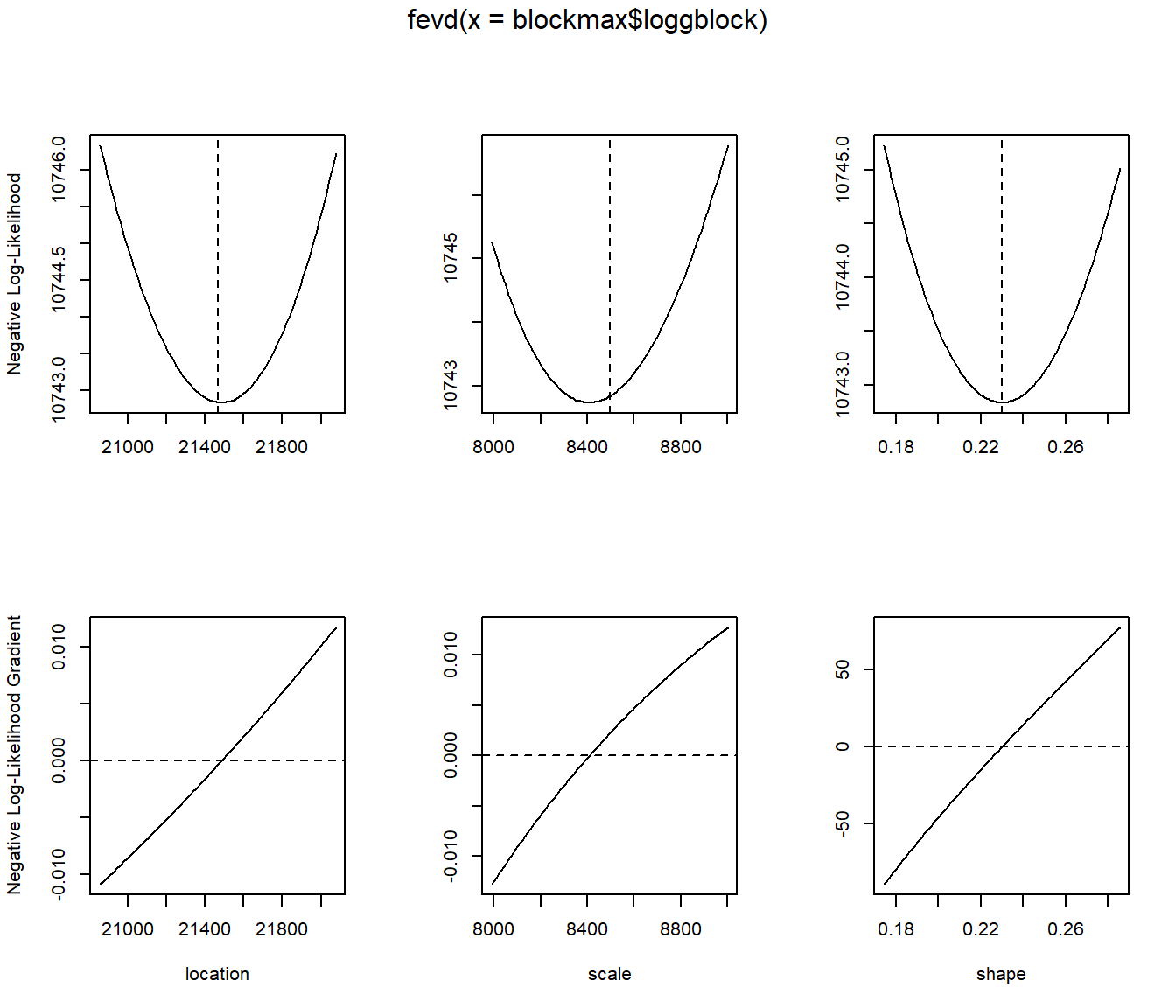
Case study - choice of block size #
Remember that
- the larger the block, the closer we are to the limiting distribution
(this is good)
However
- the larger the block, the least data we have
(this is bad)
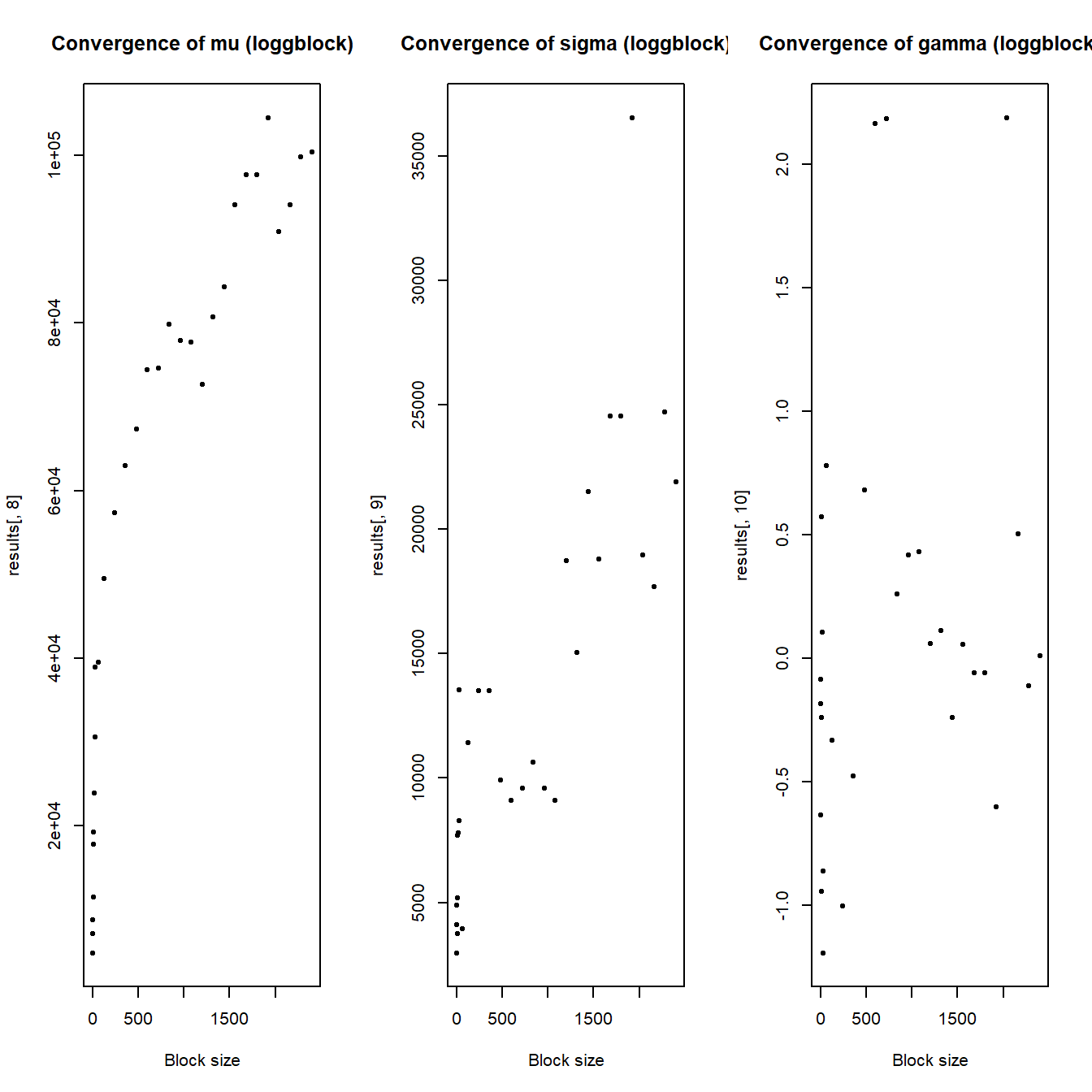
Here we aim to illustrate the impact on the parameter estimates of increasing block sizes.
Convergence with increasing block sizes #
# block sizes
blocksizes <- c(1, 2, 3, 4, 6, 12, 18, 24, 30, 60, c(1:20 * 120))
results <- c()
for (i in blocksizes) {
# number of full blocks to work with
numbers <- floor(length(claims$beta)/max(blocksizes))
# trimming claims vector
claims_trimmed <- claims[1:(numbers * i), ]
# block maxima
claims_trimmed$block <- (claims_trimmed$month - 1)%/%i +
1
blockmax2 <- tibble(betablock2 = aggregate(beta ~ block,
claims_trimmed, max)$beta, gammblock2 = aggregate(gamm ~
block, claims_trimmed, max)$gamm, loggblock2 = aggregate(logg ~
block, claims_trimmed, max)$logg)
# fitting
fit.beta2 <- fevd(blockmax2$betablock2)
fit.gamm2 <- fevd(blockmax2$gammblock2)
fit.logg2 <- fevd(blockmax2$loggblock2)
results <- rbind(results, c(i, as.double(fit.beta2$results$par[1:3]),
as.double(fit.gamm2$results$par[1:3]), as.double(fit.logg2$results$par[1:3])))
}
par(mfrow = c(1, 3))
plot(results[, 1], results[, 2], pch = 20, main = "Convergence of mu (betablock)",
xlab = "Block size")
plot(results[, 1], results[, 3], pch = 20, main = "Convergence of sigma (betablock)",
xlab = "Block size")
plot(results[, 1], results[, 4], pch = 20, main = "Convergence of gamma (betablock)",
xlab = "Block size")
par(mfrow = c(1, 3))
plot(results[, 1], results[, 5], pch = 20, main = "Convergence of mu (gammblock)",
xlab = "Block size")
plot(results[, 1], results[, 6], pch = 20, main = "Convergence of sigma (gammblock)",
xlab = "Block size")
plot(results[, 1], results[, 7], pch = 20, main = "Convergence of gamma (gammblock)",
xlab = "Block size")
par(mfrow = c(1, 3))
plot(results[, 1], results[, 8], pch = 20, main = "Convergence of mu (loggblock)",
xlab = "Block size")
plot(results[, 1], results[, 9], pch = 20, main = "Convergence of sigma (loggblock)",
xlab = "Block size")
plot(results[, 1], results[, 10], pch = 20, main = "Convergence of gamma (loggblock)",
xlab = "Block size")
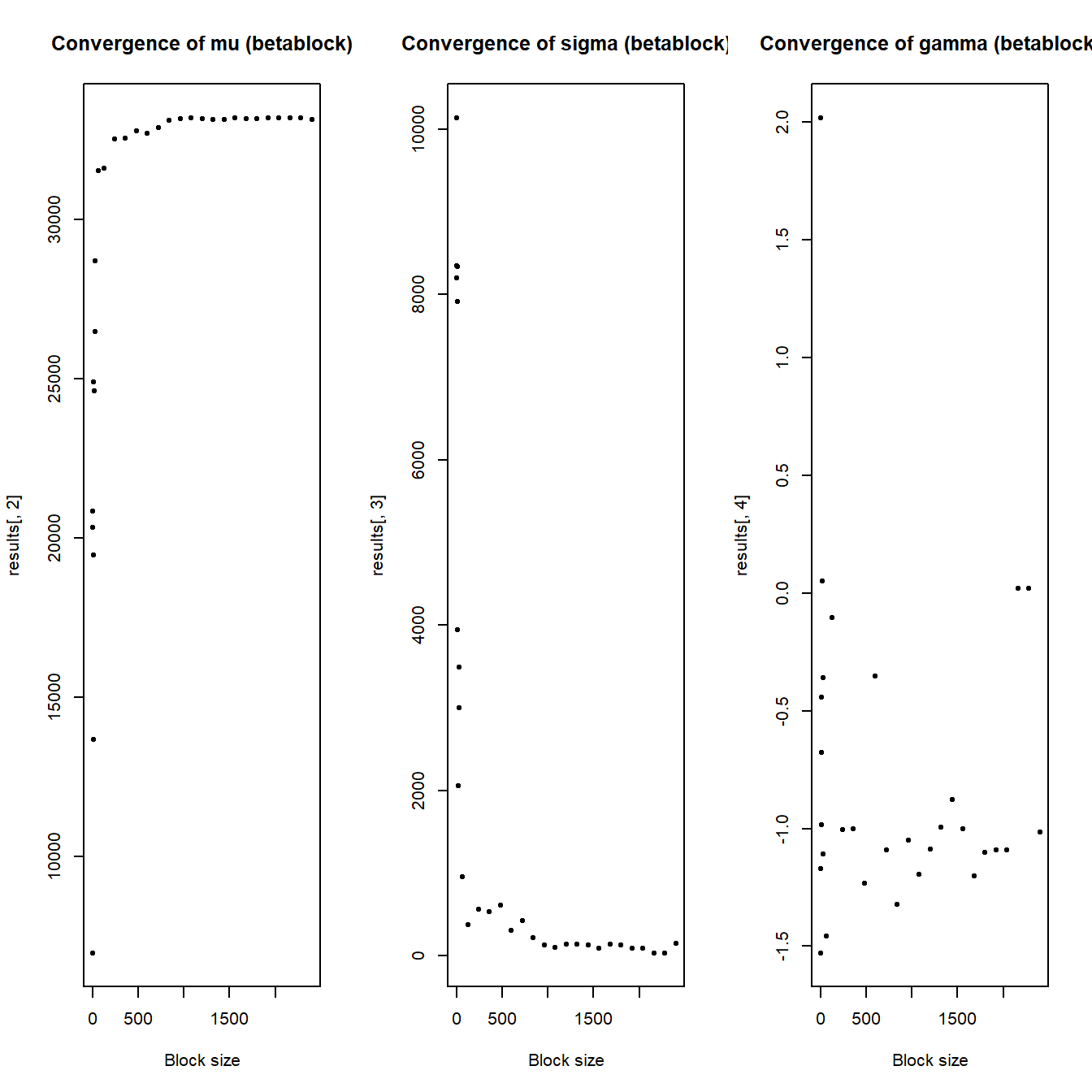
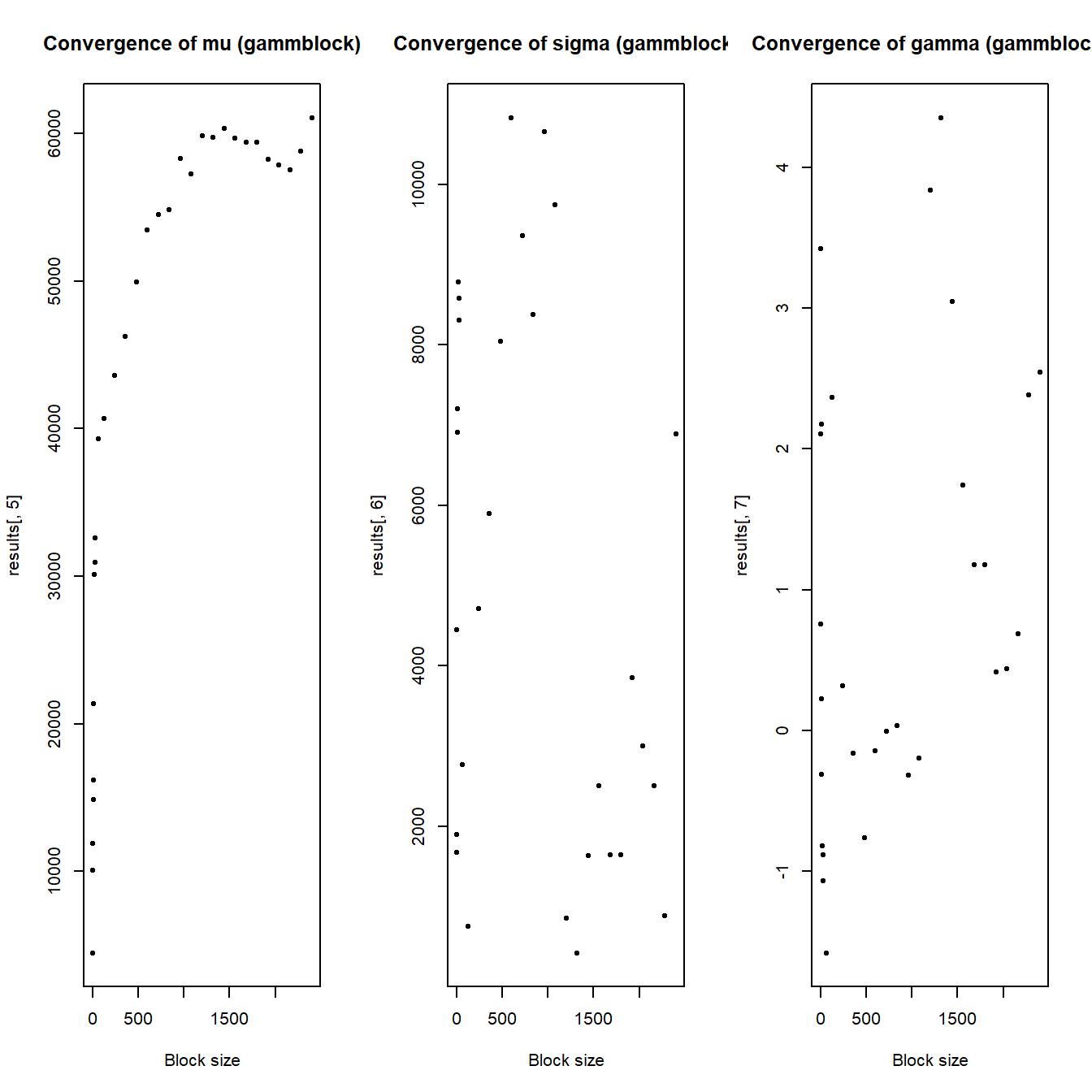
Moments #
Let
| Emp Mean | Emp Variance | Theo Mean | Theo Variance | |
|---|---|---|---|---|
| beta | 26606.41 | 18381480 | 26475.58 | 18584454 |
| gamm | 28141.08 | 222758930 | 28242.00 | 249582072 |
| logg | 28586.58 | 239426765 | 28842.05 | 280329757 |
(Empirical moments are calculated from the data,
Theoretical are calculated with parameters estimates as per above)
PML and quantiles #
PML #
- Since actual maxima can become infinite in insurance (in practical terms), we need to find a “reasonable” maximum to work with for capital and (mitigation) investment purposes (cost-benefit analysis)
- The question of “how bad” the losses can get cannot be disentangled from frequency, as the longer the timeframe, the bigger the losses can be
- The answer is called a “probable maximum loss” (PML). It has a probability (or frequency) attached to it.
Example #

“Brisbane River Strategic Floodplain Management Plan” (Queensland Reconstruction Autority (2019))
“AEP” = “Annual Exceedance Proability”
- Imagine you are focused on yearly outcomes, and that you want to estimate the outcome that you would ****** will happen ****** no more often than every 200 years (such as in solvency requirements in Australia)
- This is a “one-in-200-years” event, and is referred to as “$t$-year event” (where
- This is what we will use to calculate a PML of corresponding probability
- This is obviously impossible to estimate from data for large
- And this is even ignoring non stationarity (e.g., climate change)
- Note that that a
- The probability that a 200-year event will happen within the next 10 years is as high as
1-pbinom(0,10,1/200) - The probability that it will happen more than twice in the next 50 years is
1-pbinom(1,20,1/200) - These calculations become even more dramatic with slightly lower frequency events (1-in-100 or 1-in-50 year events)
- The probability that a 200-year event will happen within the next 10 years is as high as
Example #

“Brisbane River Strategic Floodplain Management Plan” (Queensland Reconstruction Autority (2019))
Caution: what are you modelling? #
- Although it is possible to get
- It is not clear how to aggregate the maximum of a single loss to the maximum of a whole portfolio
- Because of this, the above results are generally used to model outcomes of the peril (e.g. flood level), not losses. Damages are subsequently mapped into aggregate losses
- The interpretation and fitting is easier in that context
- for instance climate data, where you have daily maximum temperatures, and you may want to get a maximum with 200 day return period
- furthermore, the R package allows for seasonality
Quantiles #
For
Close examination of those formulas tells us that the curvature of
Case study - quantiles #
First, note that empirical
ret.per <- c(10, 50, 100, 200, 500)
Xnn <- cbind(beta = sort(claims$beta, decreasing = TRUE), gamm = sort(claims$gamm,
decreasing = TRUE), logg = sort(claims$logg, decreasing = TRUE))
empquant <- data.frame(Xnn[length(claims$beta) * 1/ret.per, ])
rownames(empquant) <- ret.per
empquant
## beta gamm logg
## 10 24308.60 21986.51 19253.06
## 50 30526.74 35395.89 35621.35
## 100 31753.68 40474.56 44351.62
## 200 32235.67 45118.02 54439.08
## 500 32790.91 53731.02 71437.34
These are not to be compared with the quantiles of the GEV.
The GEV models the distribution of maxima.
Empirical quantiles in the blocks:
Xnn2 <- cbind(betablock = sort(blockmax$betablock, decreasing = TRUE),
gammblock = sort(blockmax$gammblock, decreasing = TRUE),
loggblock = sort(blockmax$loggblock, decreasing = TRUE))
empquantblock <- data.frame(Xnn2[length(blockmax$betablock) *
1/ret.per, ])
rownames(empquantblock) <- ret.per
empquantblock
## betablock gammblock loggblock
## 10 31845.47 41496.29 45836.54
## 50 32869.52 55387.21 74562.03
## 100 33042.45 59653.57 88275.45
## 200 33186.66 63289.25 99494.12
## 500 33249.33 78734.31 138514.02
Theoretical quantiles in the blocks (maxima):
parm <- cbind(as.double(fit.beta$results$par[1:3]), as.double(fit.gamm$results$par[1:3]),
as.double(fit.logg$results$par[1:3]))
ut.theo <- data.frame(cbind(beta = parm[1, 1] + parm[2, 1]/parm[3,
1] * ((-1/(log(1 - 1/ret.per)))^parm[3, 1] - 1), gamm = parm[1,
2] + parm[2, 2]/parm[3, 2] * ((-1/(log(1 - 1/ret.per)))^parm[3,
2] - 1), logg = parm[1, 3] + parm[2, 3]/parm[3, 3] * ((-1/(log(1 -
1/ret.per)))^parm[3, 3] - 1)))
rownames(ut.theo) <- ret.per
ut.theo
## beta gamm logg
## 10 31436.86 42084.41 46508.37
## 50 32707.95 54693.10 75140.65
## 100 32964.40 59873.26 90920.27
## 200 33132.46 64947.90 109373.87
## 500 33269.71 71513.08 138703.54
Now this can be done with extRemes (with confidence intervals!)
return.level(fit.beta, return.period = ret.per, do.ci = TRUE)
...
## 95% lower CI Estimate 95% upper CI
## 10-year return level 31263.52 31436.86 31610.19
## 50-year return level 32573.09 32707.95 32842.81
## 100-year return level 32821.90 32964.40 33106.90
## 200-year return level 32978.01 33132.46 33286.90
## 500-year return level 33099.84 33269.71 33439.57
...
return.level(fit.gamm, return.period = ret.per, do.ci = TRUE)
...
## 95% lower CI Estimate 95% upper CI
## 10-year return level 40867.26 42084.41 43301.56
## 50-year return level 52139.71 54693.10 57246.48
## 100-year return level 56484.68 59873.26 63261.84
## 200-year return level 60578.48 64947.90 69317.31
## 500-year return level 65635.36 71513.08 77390.81
...
return.level(fit.logg, return.period = ret.per, do.ci = TRUE)
...
## 95% lower CI Estimate 95% upper CI
## 10-year return level 44199.82 46508.37 48816.91
## 50-year return level 68082.59 75140.65 82198.71
## 100-year return level 80241.17 90920.27 101599.36
## 200-year return level 93750.30 109373.87 124997.45
## 500-year return level 113913.35 138703.54 163493.72
...
Theoretical figures are close to the empirical ones (as they should!), but obviously the theoretical versions are smoothed and will be less likely to underestimate extreme events, especially in high return level figures (which are more prone to sampling issues in the empirical data).
Generalised Pareto distribution #
Asymptotic properties of the tails #
Main result: Asymptotic properties of the tails #
- Let us now consider a distribution
- If we were pricing an excess of loss (or stop loss on a portfolio), the attachment point or retention level or limit could be expressed as a
- The tail is the distribution beyond this point. We characterise the tail with the help of the distribution function of the excess over threshold
- The main result is that, for high
between both distributions is asymptotically zero)
The GP distribution #
Generalised Pareto distribution #
- The Generalised Pareto distribution function is given by
- We distinguish again three cases:
GP df #

GP pdf #
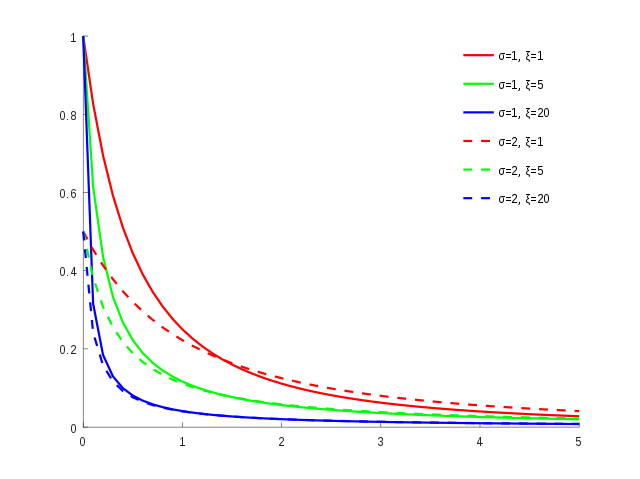
Moments #
The first central moments of
Note:
- The first four
Estimation #
Estimation: choice of threshold
We seek to estimate the tail (remember Tutorial Exercise NLI11)
- Probability of exceeding
- Then for given value of
(as the result is an asymptotic result for
Estimation: choice of threshold
The choice of
- larger
- but larger
The choice is often also based on the following further considerations:
- mean-excess plot: Pareto should be linear (slope same sign as
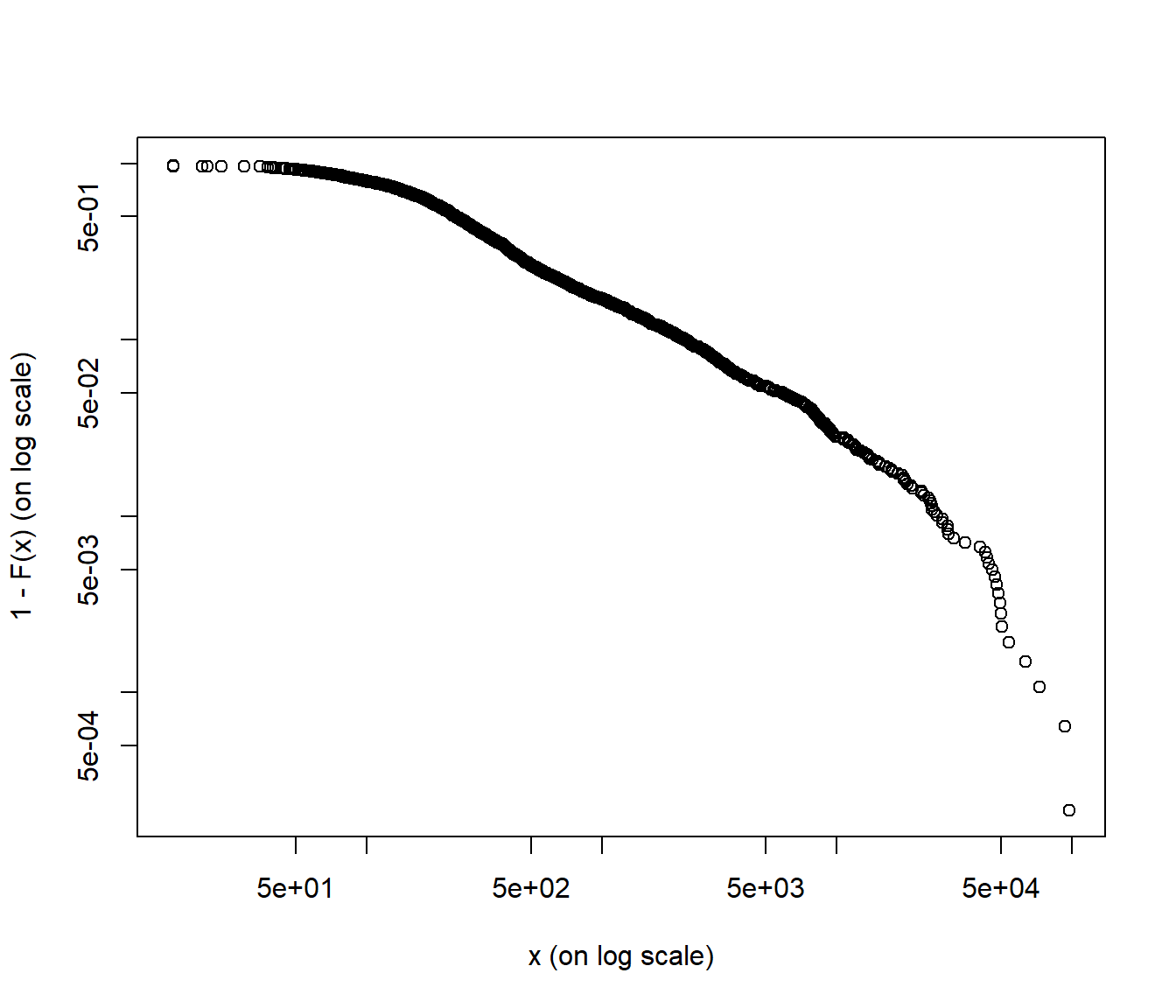
- empirical df on a doubly logarithmic scale: Pareto should be linear
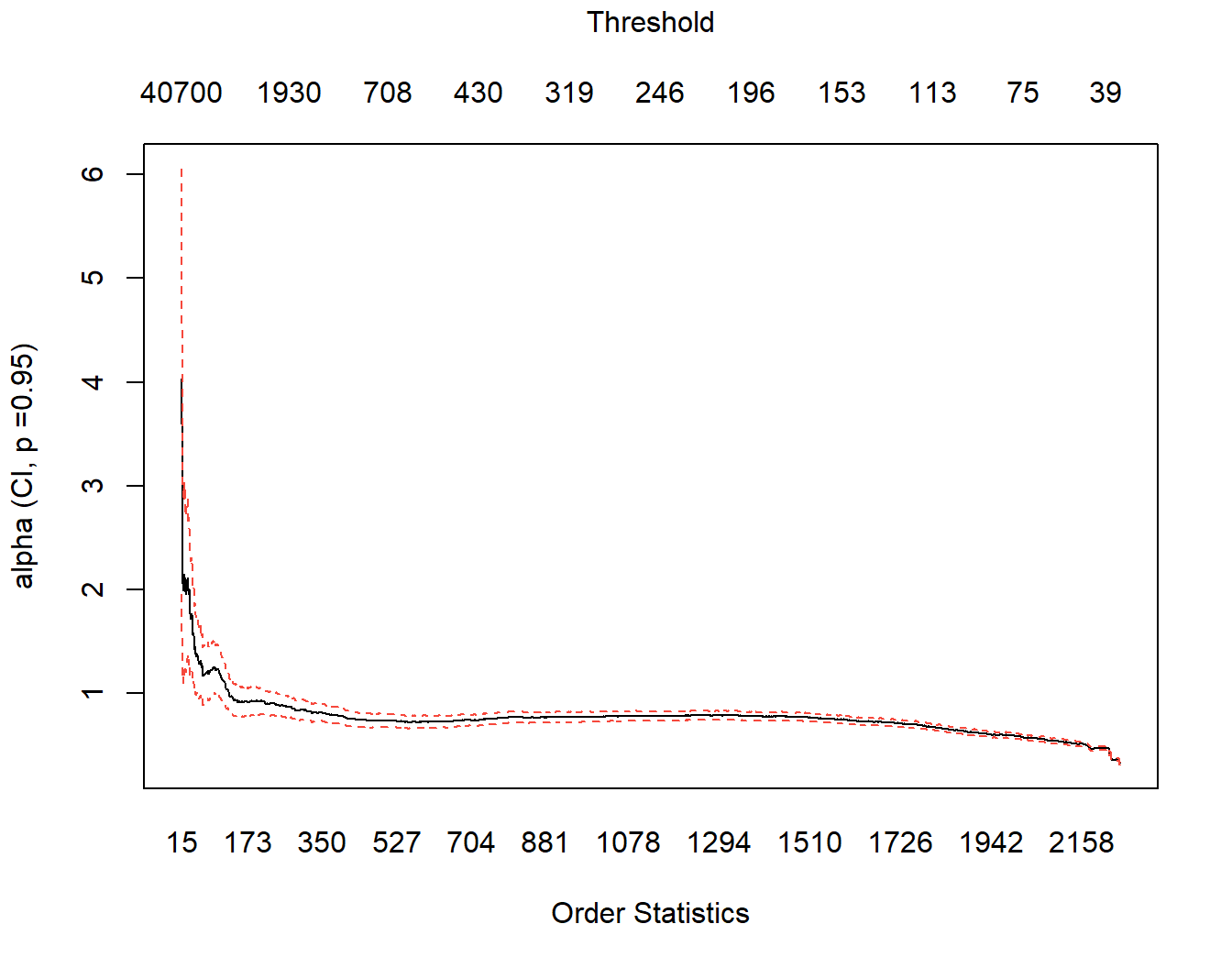
- Hill plot (Wuthrich (2023), p. 76): stability of Pareto parameter
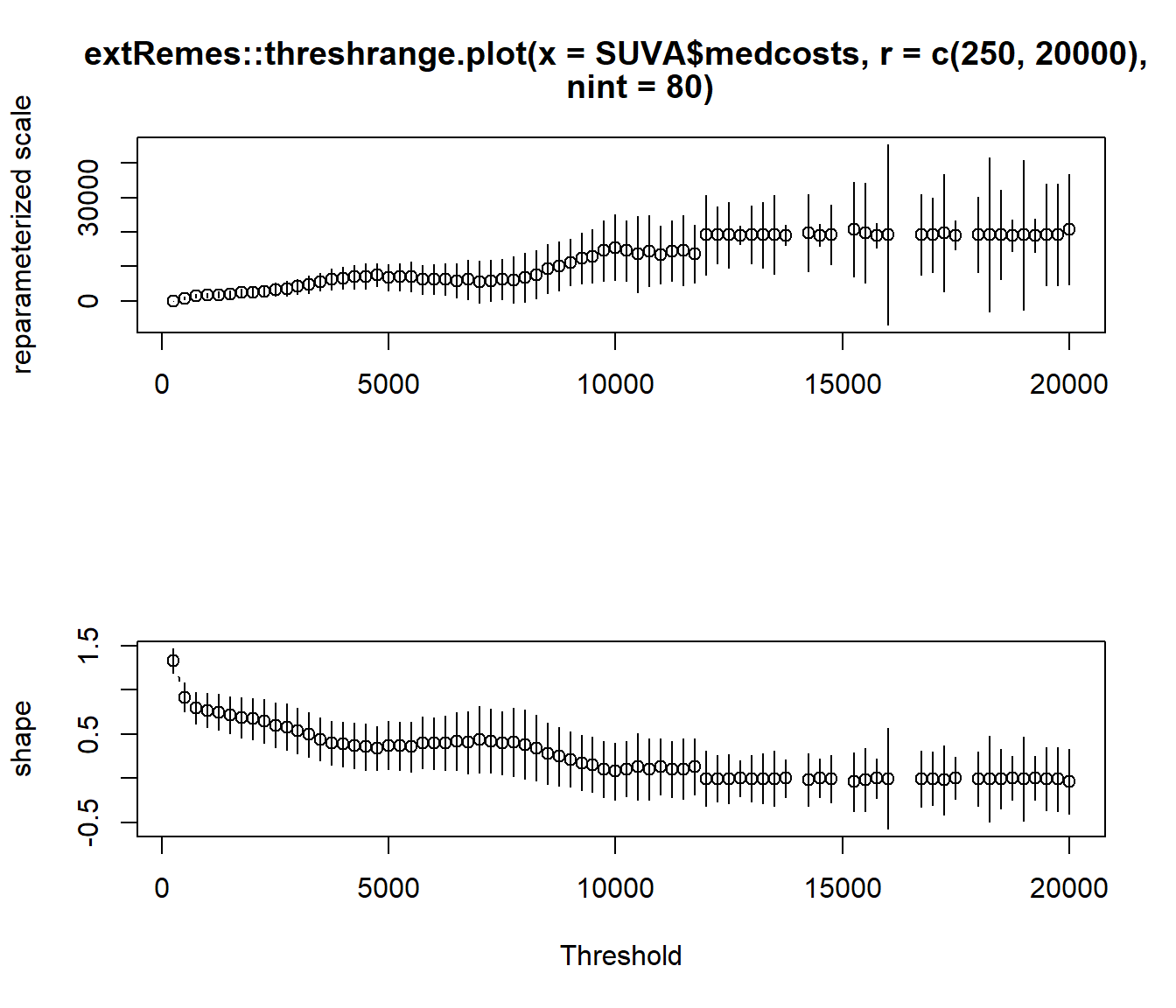
- stability of
extRemespackage does that automatically) - goodness of fit for different choices of
Unfortunately there is no “optimal” (or “automatic”) procedure for choosing
Case study #
Case study: workers compensation medical costs #
- Example of real actuarial data from Avanzi, Cassar, and Wong (2011)
- Data were provided by the SUVA (Swiss workers compensation insurer)
- Random sample of 5% of accident claims in construction sector with accident year 1999 (developped as of 2003)
- Claims are medical costs
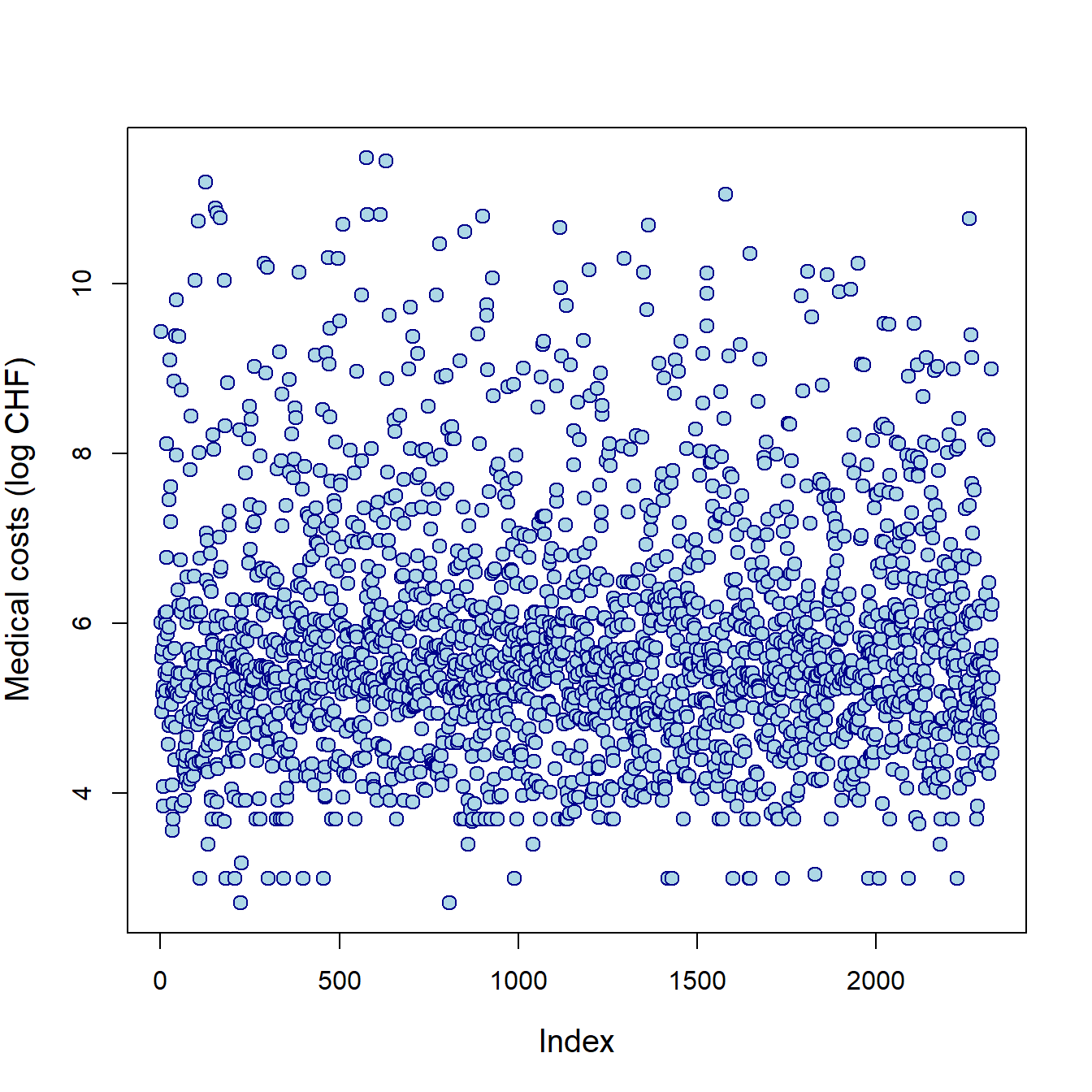
- In Avanzi, Cassar, and Wong (2011) we model those claims with a Gumbel distribution, which suggests heavy tails, which is confirmed by the following graphs. This, however, wasn’t the main objective of the paper, but was good enough for our purposes.
SUVA <- read_excel("SUVA.xls")
as_tibble(SUVA)
...
## # A tibble: 2,326 × 2
## medcosts dailyallow
## <dbl> <dbl>
## 1 407 0
## 2 12591 13742
...
Data exploration #
plot(SUVA$medcosts, ylab = "Medical costs (CHF)", cex = 1.25,
cex.lab = 1.25, col = "darkblue", bg = "lightblue", pch = 21)

plot(log(SUVA$medcosts), ylab = "Medical costs (log CHF)", cex = 1.25,
cex.lab = 1.25, col = "darkblue", bg = "lightblue", pch = 21)
extRemes::qqnorm(log(SUVA$medcosts), cex.lab = 1.25)

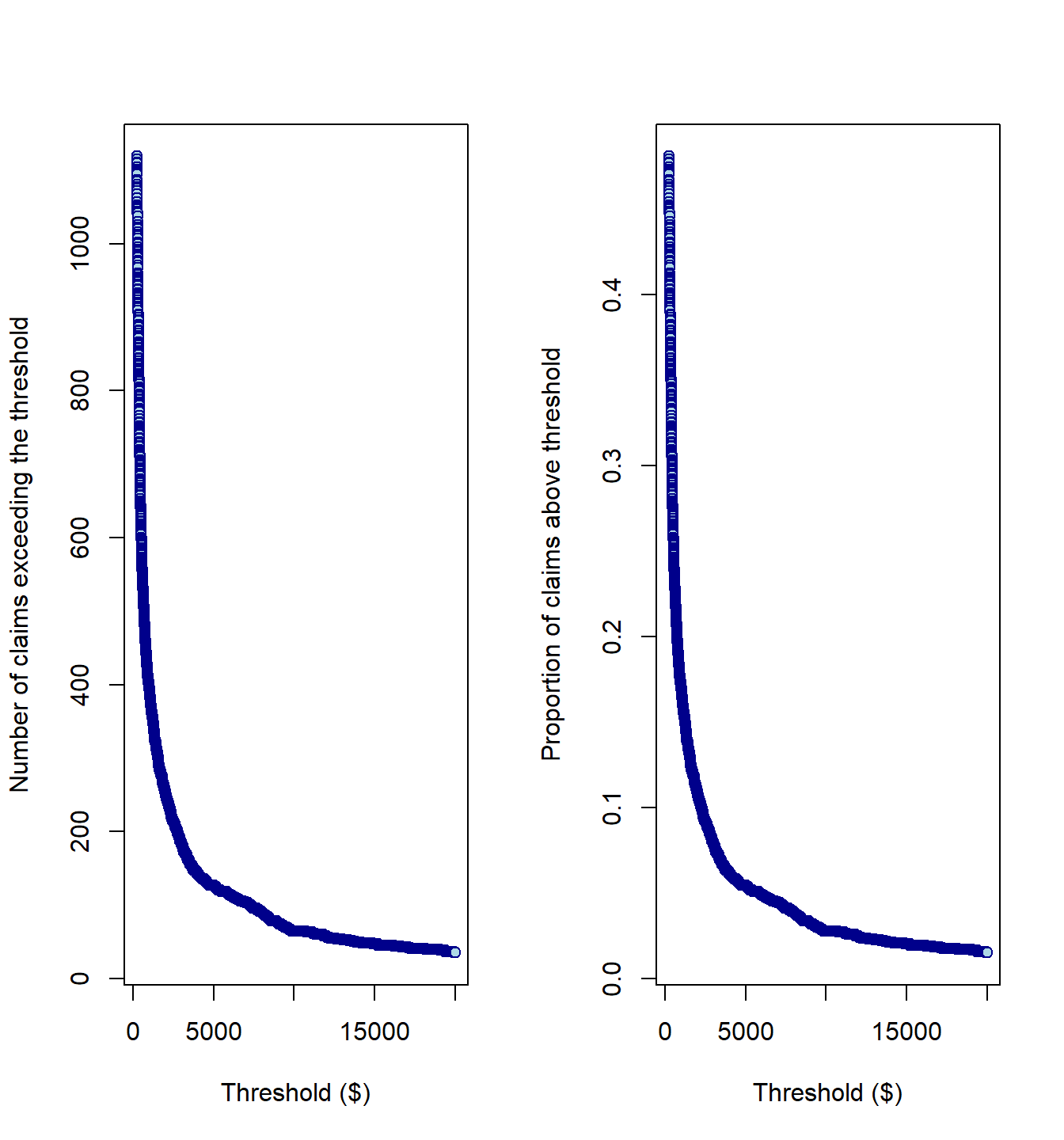
Size of tail #
numbexc <- c()
for (i in 250:20000) {
numbexc <- c(numbexc, length(SUVA$medcosts[SUVA$medcosts >
i]))
}
par(mfrow = c(1, 2))
plot(250:20000, numbexc, xlab = "Threshold ($)", ylab = "Number of claims exceeding the threshold",
col = "darkblue", bg = "lightblue", pch = 21)
plot(250:20000, numbexc/length(SUVA$medcosts), xlab = "Threshold ($)",
ylab = "Proportion of claims above threshold", col = "darkblue",
bg = "lightblue", pch = 21)
Mean-excess plot #
extRemes::mrlplot(SUVA$medcosts, xlim = c(250, 20000))
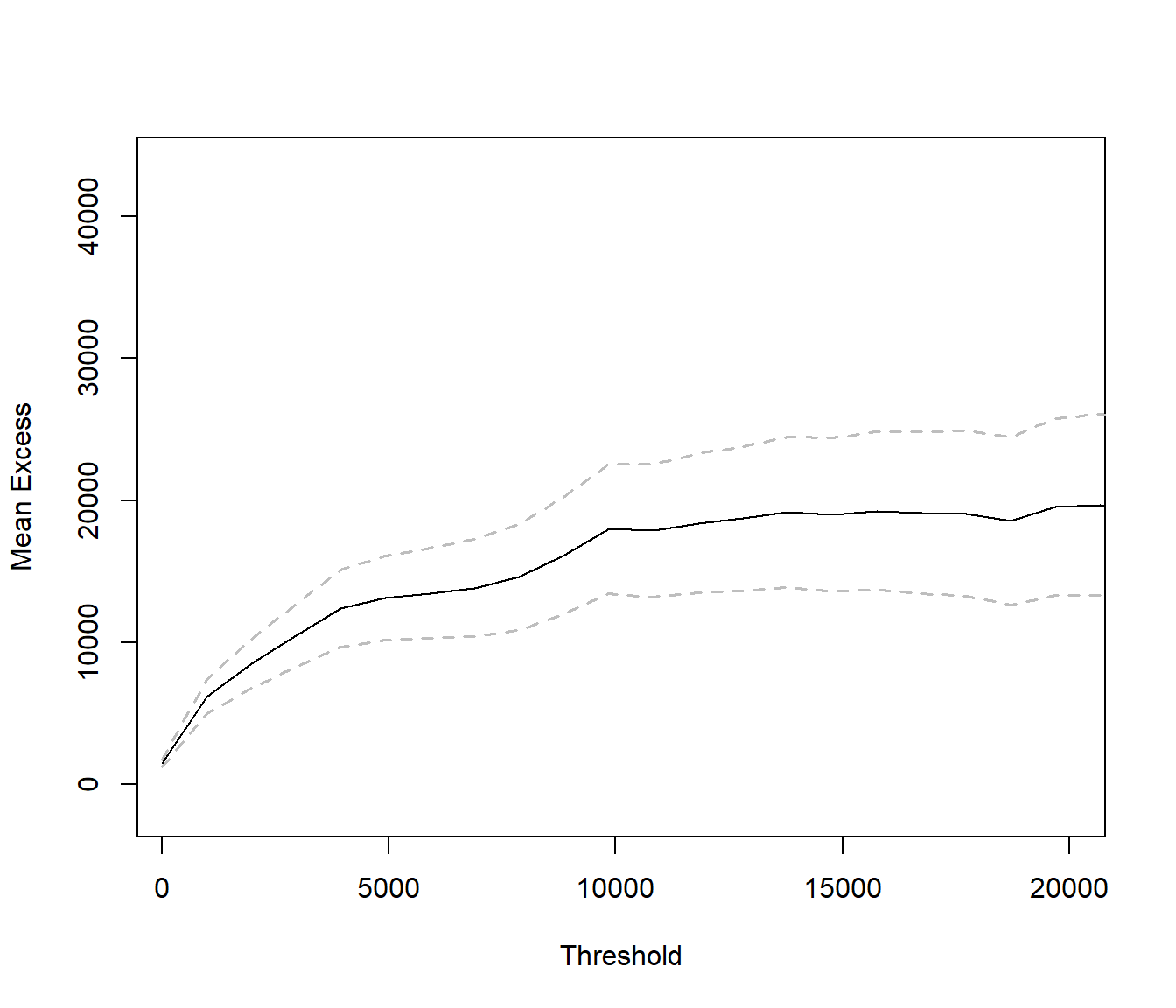
Empirical
evir::emplot(SUVA$medcosts, alog = "xy", labels = TRUE)
Hill plot #
evir::hill(SUVA$medcosts)
Stability of
extRemes::threshrange.plot(SUVA$medcosts, r = c(250, 20000),
nint = 80)
Estimation results for
fit.SUVA.500 <- fevd(SUVA$medcosts, threshold = 500, type = "GP",
time.units = "1/year")
fit.SUVA.500
...
## Estimated parameters:
## scale shape
## 1272.3550452 0.9193739
##
## Standard Error Estimates:
## scale shape
## 126.8004198 0.0849976
##
## Estimated parameter covariance matrix.
## scale shape
## scale 16078.346449 -6.336002009
## shape -6.336002 0.007224592
##
## AIC = 11006.09
##
## BIC = 11014.93
...
numbexc[501 - 250] # n_u noting numbexc[1] = n_250
## [1] 616
numbexc[501 - 250]/length(SUVA$medcosts)
## [1] 0.2648323
plot(fit.SUVA.500)
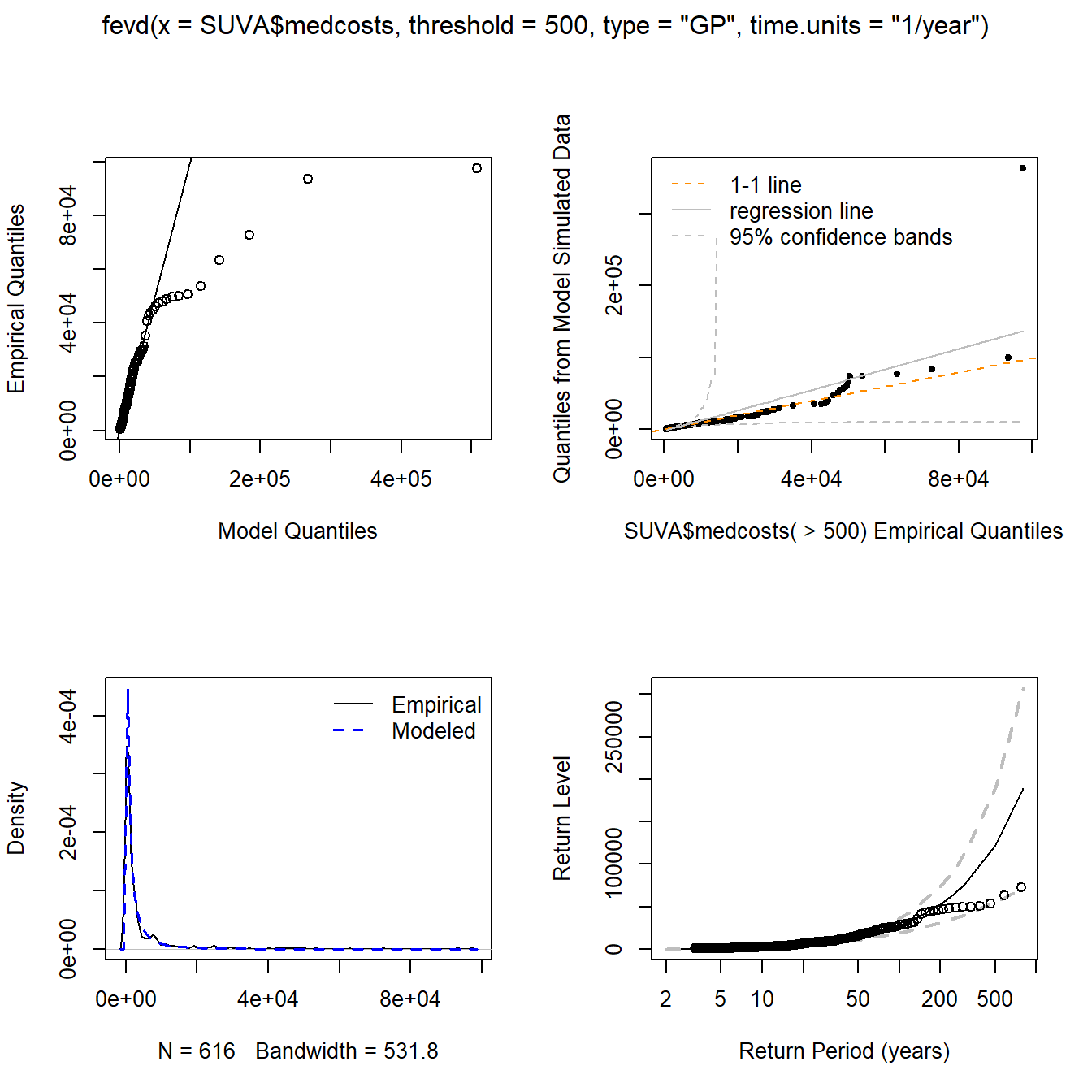
Estimation results for
fit.SUVA.5500 <- fevd(SUVA$medcosts, threshold = 5500, type = "GP",
time.units = "1/year")
fit.SUVA.5500
...
## Estimated parameters:
## scale shape
## 9080.1415439 0.3582073
##
## Standard Error Estimates:
## scale shape
## 867.9692478 0.1180018
##
## Estimated parameter covariance matrix.
## scale shape
## scale 753370.61513 -48.21705582
## shape -48.21706 0.01392443
##
## AIC = 2474.628
##
## BIC = 2480.169
...
numbexc[5501 - 250] # n_u
## [1] 118
numbexc[5501 - 250]/length(SUVA$medcosts)
## [1] 0.05073087
plot(fit.SUVA.5500)
Estimation results for
fit.SUVA.9500 <- fevd(SUVA$medcosts, threshold = 9500, type = "GP",
time.units = "1/year")
fit.SUVA.9500
...
## Estimated parameters:
## scale shape
## 1.439198e+04 1.531774e-01
##
## Standard Error Estimates:
## scale shape
## 1105.107349 0.120504
##
## Estimated parameter covariance matrix.
## scale shape
## scale 1221262.25328 -52.03034314
## shape -52.03034 0.01452121
##
## AIC = 1510.063
##
## BIC = 1514.56
...
numbexc[9501 - 250] # n_u
## [1] 70
numbexc[9501 - 250]/length(SUVA$medcosts)
## [1] 0.03009458
plot(fit.SUVA.9500)
Estimation results for
fit.SUVA.12500 <- fevd(SUVA$medcosts, threshold = 12500, type = "GP",
time.units = "1/year")
fit.SUVA.12500
...
## Estimated parameters:
## scale shape
## 1.905240e+04 -5.131924e-03
##
## Standard Error Estimates:
## scale shape
## 2240.8326877 0.1206834
##
## Estimated parameter covariance matrix.
## scale shape
## scale 5021331.1344 -147.94884187
## shape -147.9488 0.01456447
##
## AIC = 1195.941
##
## BIC = 1199.956
...
numbexc[12501 - 250] # n_u
## [1] 55
numbexc[12501 - 250]/length(SUVA$medcosts)
## [1] 0.02364574
plot(fit.SUVA.12500)
Measures of tail weight #
- Existence of moments (e.g. gamma vs Pareto)
- Limiting density ratios: relative value of density functions at the far end of the upper tail of two distributions
- Hazard rates
- Log-log plot: linear decrease for heavy tails
- Mean excess function: linear increase for heavy tails
Limiting density ratios: gamma example #
plot(1:10000/1000, dgamma(1:10000/1000, shape = 0.75, rate = 0.75)/dexp(1:10000/1000,
1), xlab = "x", main = "ratio of densities gamma(alpha,beta) to exponential(1)",
ylab = "", type = "l", col = "blue", ylim = c(0, 3.5), xlim = c(0,
6), lwd = 2, cex = 1.5)
text(5.5, 2, "alpha=beta=0.75", col = "blue", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 1, rate = 1)/dexp(1:10000/1000,
1), type = "l", col = "black", lwd = 2)
text(5.5, 1.2, "alpha=beta=1", col = "black", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 2, rate = 2)/dexp(1:10000/1000,
1), type = "l", col = "red", lwd = 2)
text(5.5, 0.3, "alpha=beta=2", col = "red", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 10, rate = 10)/dexp(1:10000/1000,
1), type = "l", col = "green", lwd = 2)
text(2.8, 0.2, "alpha=beta=10", col = "green", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 0.5, rate = 0.5)/dexp(1:10000/1000,
1), type = "l", col = "magenta", lwd = 2)
text(5.5, 3.5, "alpha=beta=0.5", col = "magenta", cex = 1.5)
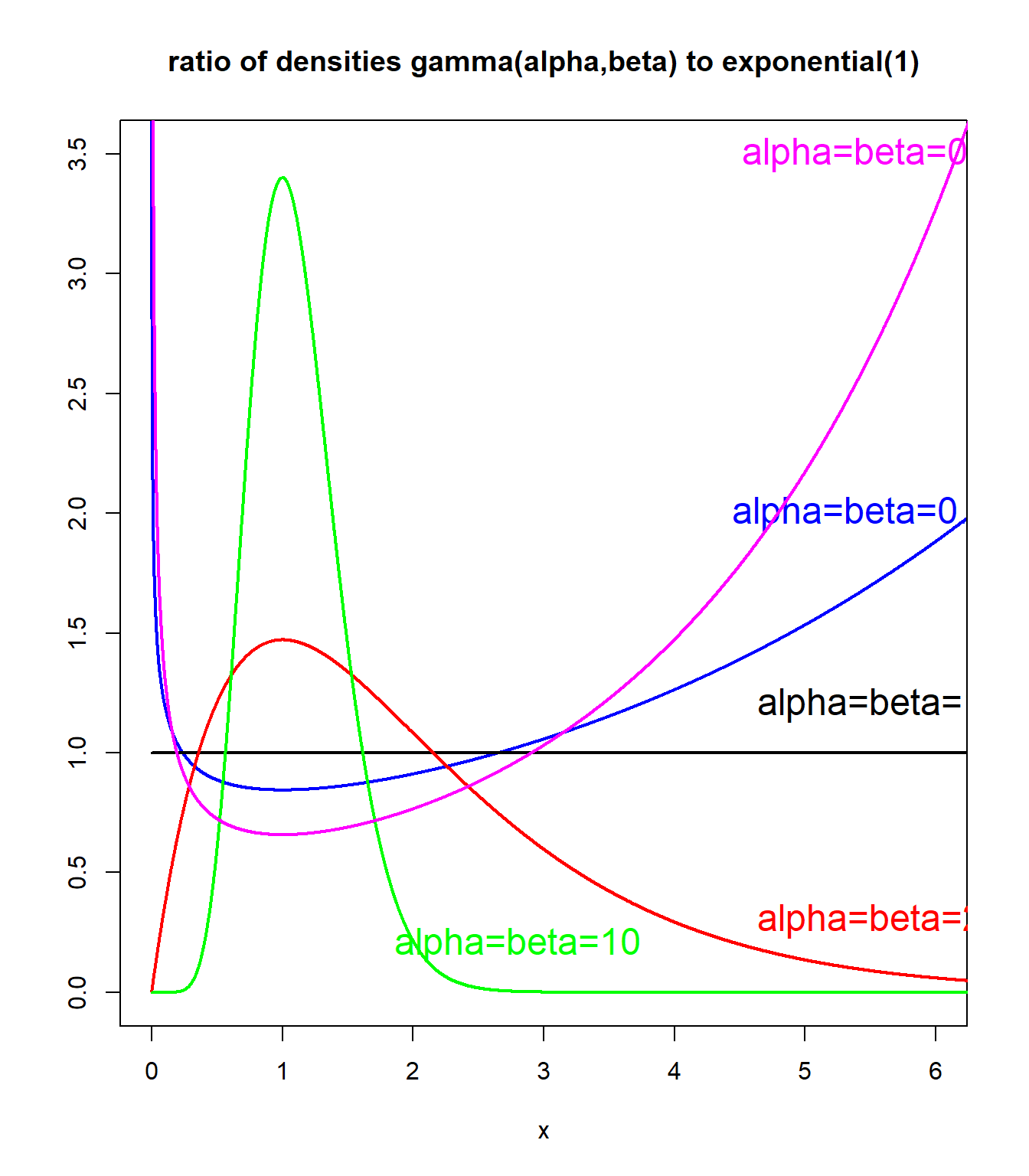
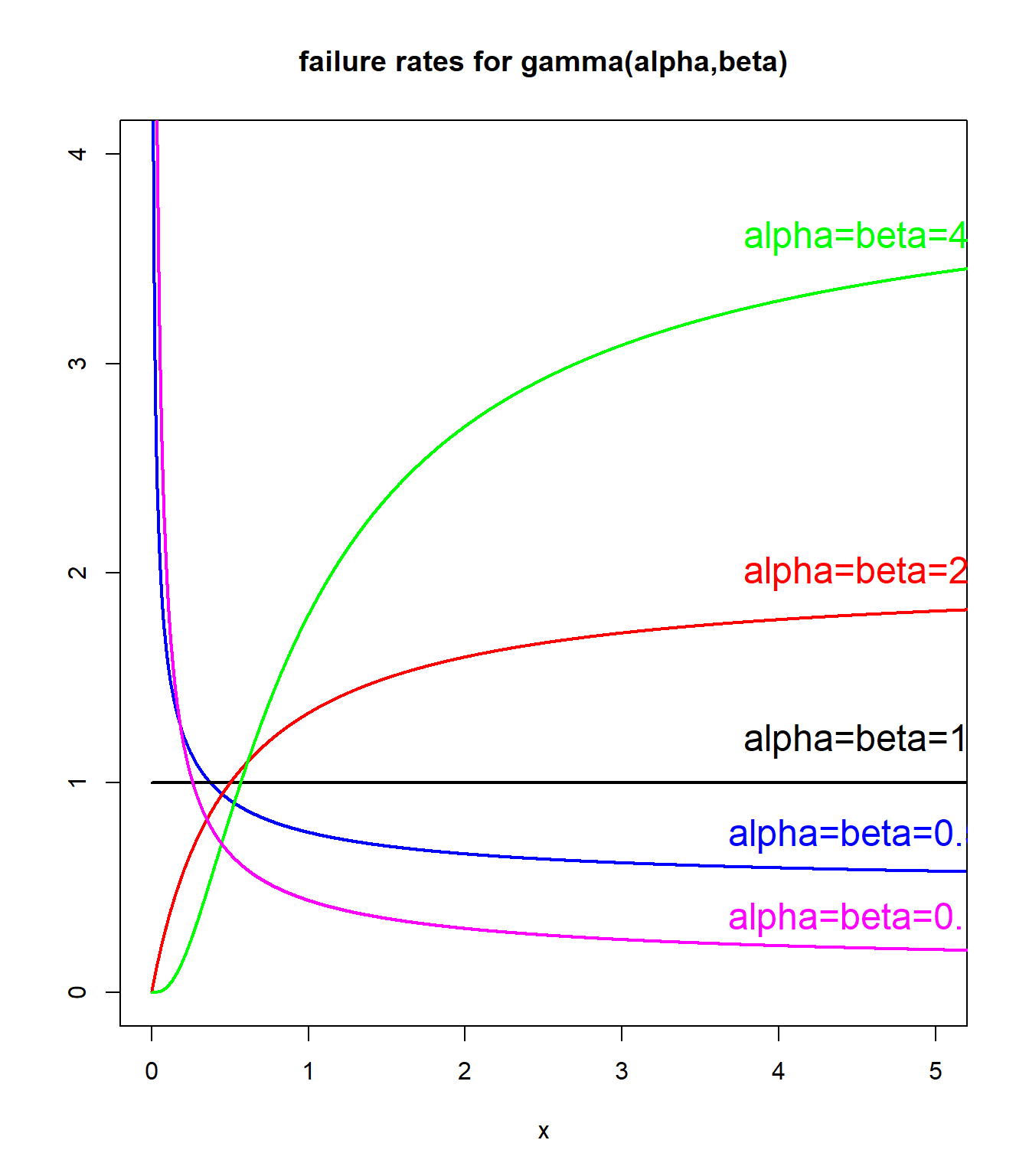
Hazard rates: gamma example with fixed mean #
plot(1:10000/1000, dgamma(1:10000/1000, shape = 0.5, rate = 0.5)/(1 -
pgamma(1:10000/1000, shape = 0.5, rate = 0.5)), xlab = "x",
main = "hazard rates for gamma(alpha,beta)", ylab = "", type = "l",
col = "blue", ylim = c(0, 4), xlim = c(0, 5), lwd = 2, cex = 1.5)
text(4.5, 0.75, "alpha=beta=0.5", col = "blue", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 1, rate = 1)/(1 -
pgamma(1:10000/1000, shape = 1, rate = 1)), type = "l", col = "black",
lwd = 2)
text(4.5, 1.2, "alpha=beta=1", col = "black", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 2, rate = 2)/(1 -
pgamma(1:10000/1000, shape = 2, rate = 2)), type = "l", col = "red",
lwd = 2)
text(4.5, 2, "alpha=beta=2", col = "red", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 4, rate = 4)/(1 -
pgamma(1:10000/1000, shape = 4, rate = 4)), type = "l", col = "green",
lwd = 2)
text(4.5, 3.6, "alpha=beta=4", col = "green", cex = 1.5)
lines(1:10000/1000, dgamma(1:10000/1000, shape = 0.1, rate = 0.1)/(1 -
pgamma(1:10000/1000, shape = 0.1, rate = 0.1)), type = "l",
col = "magenta", lwd = 2)
text(4.5, 0.35, "alpha=beta=0.1", col = "magenta", cex = 1.5)
References #
Avanzi, Benjamin, Luke C. Cassar, and Bernard Wong. 2011. “Modelling Dependence in Insurance Claims Processes with Lévy Copulas.” ASTIN Bulletin 41 (2): 575–609.
Embrechts, Paul, Sidney I. Resnick, and Gennady Samorodnitsky. 1999. “Extreme Value Theory as a Risk Management Tool.” North American Actuarial Journal 3 (2): 30–41.
Embrechts, P., C. Klüppelberg, and T. Mikosch. 1997. Modelling Extremal Events for Insurance and Finance. Springer, Berlin.
Gilleland, Eric, and Richard W. Katz. 2016. “extRemes 2.0: An Extreme Value Analysis Package in R.” Journal of Statistical Software 72 (8).
IoA. 2020. Course Notes and Core Reading for Subject CS2 Models. The Institute of Actuaries.
Queensland Reconstruction Autority. 2019. “Brisbane River Strategic Floodplain Management Plan.” The State of Queensland.
Wuthrich, Mario V. 2023. “Non-Life Insurance: Mathematics & Statistics.” Lecture notes. RiskLab, ETH Zurich; Swiss Finance Institute.