Dependence and multivariate modelling #
Introduction to Dependence #
Motivation #
How does dependence arise?
- Events affecting more than one variable (e.g., storm on building, car and business interruption covers)
- Underlying economic factors affecting more than one risk area (e.g., inflation, unemployment)
- Clustering/concentration of risks (e.g., household, geographical area)
Reasons for modelling dependence:
- Pricing:
- get adequate risk loadings
(note that dependence affects quantiles, not the mean)
- get adequate risk loadings
- Solvency assessment:
- bottom up: for given risks, get capital requirements
(get quantiles of aggregate quantities)
- bottom up: for given risks, get capital requirements
- Capital allocation:
- top down: for given capital, allocate portions to risk
(for profitability assessment)
- top down: for given capital, allocate portions to risk
- Portfolio structure: (or strategic asset allocation)
- how do assets and liabilities move together?
Examples #
- World Trade Centre (9/11) causing losses to Property, Life, Workers’ Compensation, Aviation insurers
- Dot.com market collapse and GFC causing losses to the stock market and to insurers of financial institutions and Directors & Officers (D&O) writers
- Asbestos affecting many past liability years at once
- Australian 2019-2020 Bushfires causing losses to Property, Life, credit, etc
- Covid-19 impacting financial markets, travel insurance, health, credit, D&O, business interruption covers, construction price inflation, etc
- El Niña and associated floods impacting property insurance in certain geographical areas, construction prices inflation, etc
Example of real actuarial data (Avanzi, Cassar, and Wong 2011) #
- Data were provided by the SUVA (Swiss workers compensation insurer)
- Random sample of 5% of accident claims in construction sector with accident year 1999 (developped as of 2003)
- 1089 of those are common (!)
- Two types of claims: 2249 medical cost claims, et 1099 daily allowance claims
SUVA <- read_excel("SUVA.xls")
# filtering and logging the common claims
SUVAcom <- log(SUVA[SUVA$medcosts > 0 & SUVA$dailyallow > 0,
])
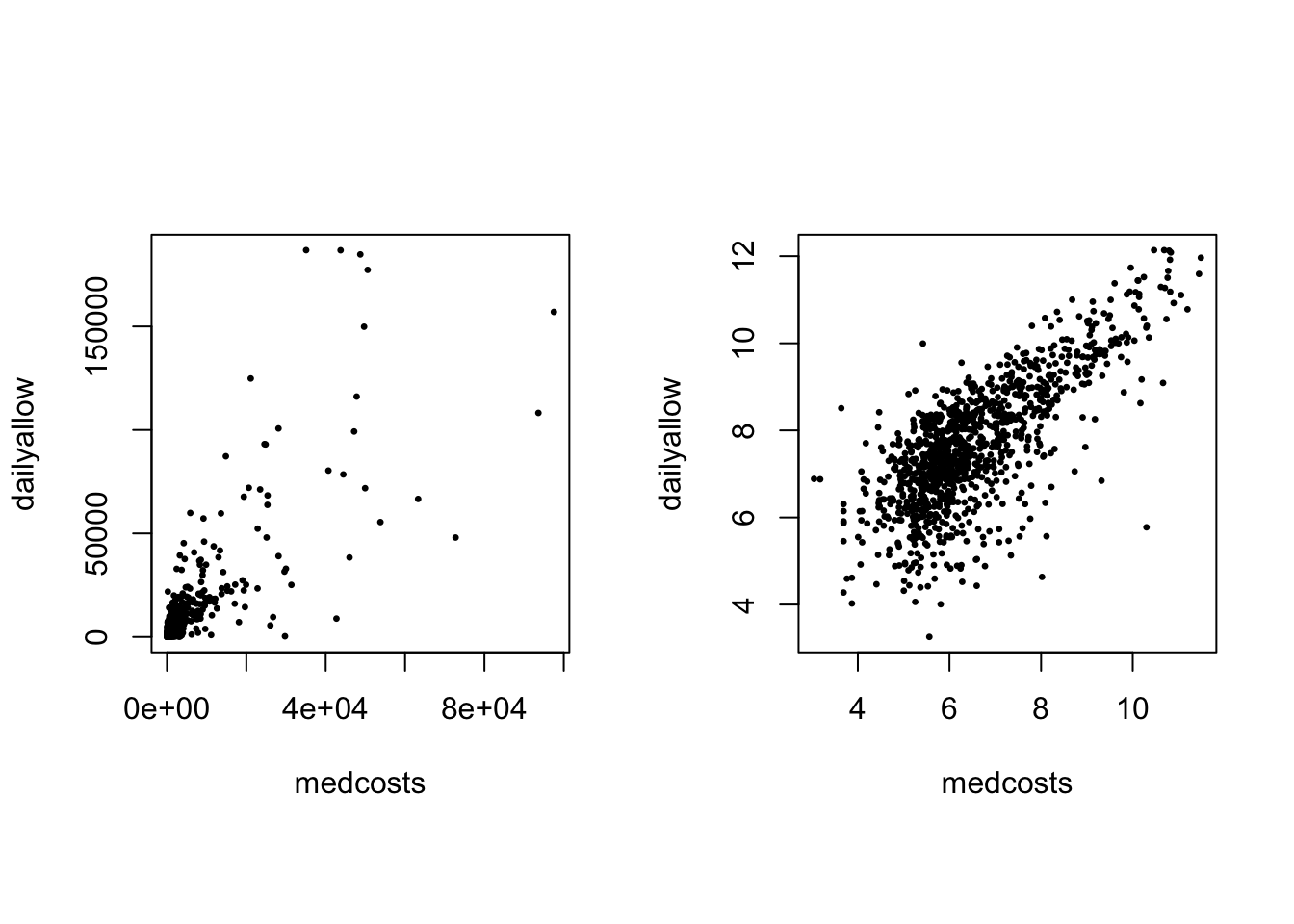
Scatterplot of those 1089 common claims (LHS) amd their log (RHS):
par(mfrow = c(1, 2), pty = "s")
plot(exp(SUVAcom), pch = 20, cex = 0.5)
plot(SUVAcom, pch = 20, cex = 0.5)
Scatterplot of the log of the 1089 common claims (LHS) and their empirical copula (ranks) (RHS):
par(mfrow = c(1, 2), pty = "s")
plot(SUVAcom, pch = 20, cex = 0.5)
plot(copula::pobs(SUVAcom)[, 1], copula::pobs(SUVAcom)[, 2],
pch = 20, cex = 0.5)
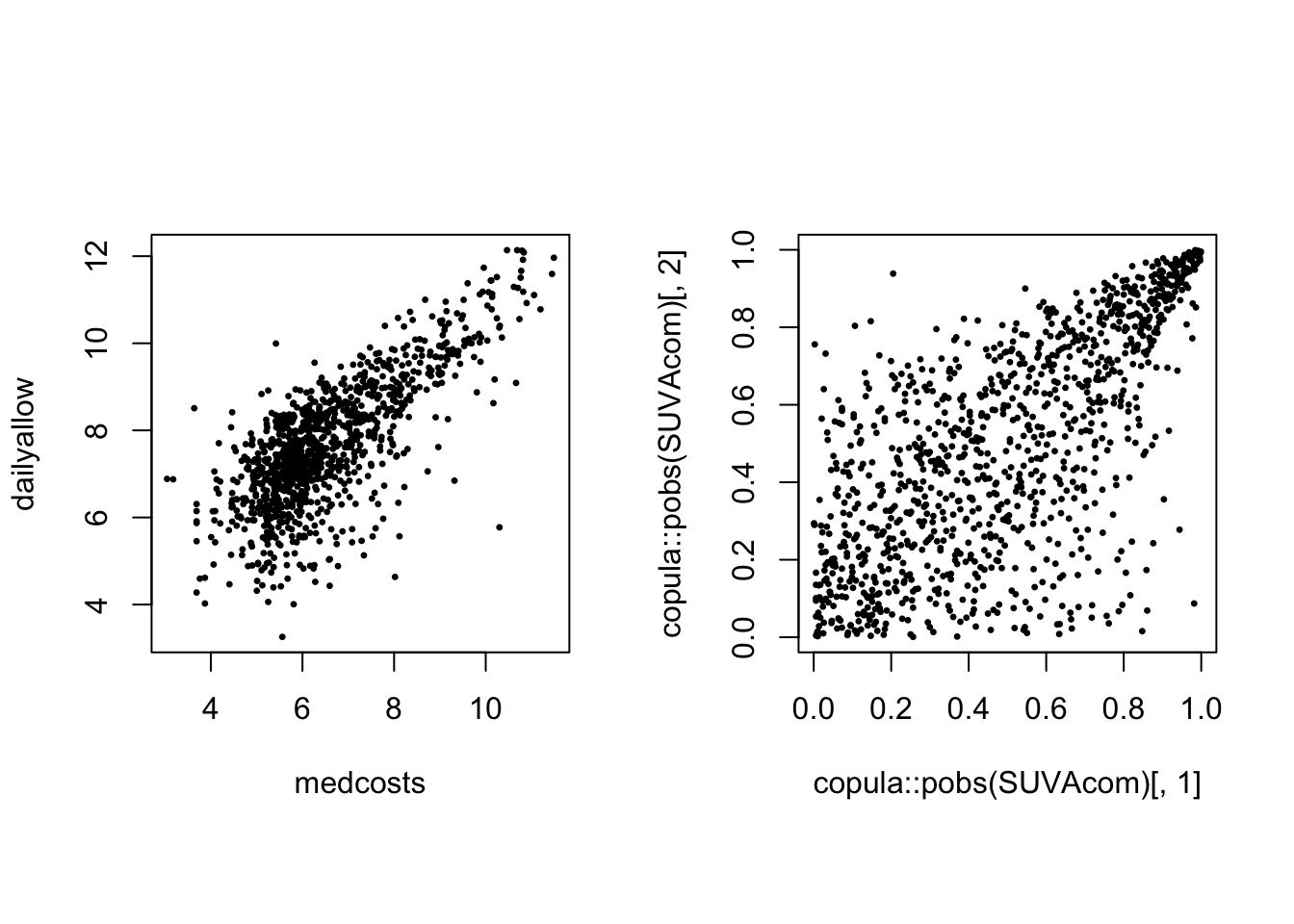
There is obvious right tail dependence.
Multivariate Normal Distributions #
The multivariate Normal distribution #
- standard Normal marginals, i.e.
- positive definite correlation matrix:
where
- if
Properties #
If
has a multivariate Normal distribution with mean
and covariance
We can construct a lower triangular matrix
such that
The matrix chol() in R).
This will be useful later on for the simulation of multivariate Gaussian random variables.
Measures of dependence #
Pearson’s correlation measure #
Pearson’s correlation coefficient is defined by
Note:
- This measures the degree of linear relationship between
- In general, it does not reveal all the information on the dependence structure of random couples.
Kendall’s tau #
Kendall’s tau correlation coefficient is defined by
where
Note:
- The first term is called the probability of concordance; the latter, probability of discordance.
- Its value is also between -1 and 1.
- It can be shown to equal:
- Concordance and discordance only depends on ranks, and this indicator is hence less affected by the marginal distributions of
than Pearson’s correlation.
(Spearman’s) rank correlation #
Spearman’s rank correlation coefficient is defined by
where
Note:
- It is indeed the Pearson’s correlation but applied to the transformed
variables
- Its value is also between -1 and 1.
- It is directly formulated on ranks, and hence is less affected by the marginal distributions of
Example: the case of multivariate Normal #
-
Pearson’s correlation:
-
Kendall’s tau:
-
Spearman’s rank correlation:
Example: SUVA data #
cor(SUVAcom, method = "pearson") # default
## medcosts dailyallow
## medcosts 1.0000000 0.7489701
## dailyallow 0.7489701 1.0000000
cor(SUVAcom, method = "kendall")
## medcosts dailyallow
## medcosts 1.0000000 0.5154526
## dailyallow 0.5154526 1.0000000
cor(SUVAcom, method = "spearman")
## medcosts dailyallow
## medcosts 1.0000000 0.6899156
## dailyallow 0.6899156 1.0000000
Repeating those on the original claims (before
cor(exp(SUVAcom), method = "pearson") # default
## medcosts dailyallow
## medcosts 1.0000000 0.8015752
## dailyallow 0.8015752 1.0000000
cor(exp(SUVAcom), method = "kendall")
## medcosts dailyallow
## medcosts 1.0000000 0.5154526
## dailyallow 0.5154526 1.0000000
cor(exp(SUVAcom), method = "spearman")
## medcosts dailyallow
## medcosts 1.0000000 0.6899156
## dailyallow 0.6899156 1.0000000
We see that Kendall’s
Limits of correlation #
Correlation = dependence? #
Correlation between the consumption of cheese and deaths by becoming tangled in bedsheets (in the US, see Vigen 2015):
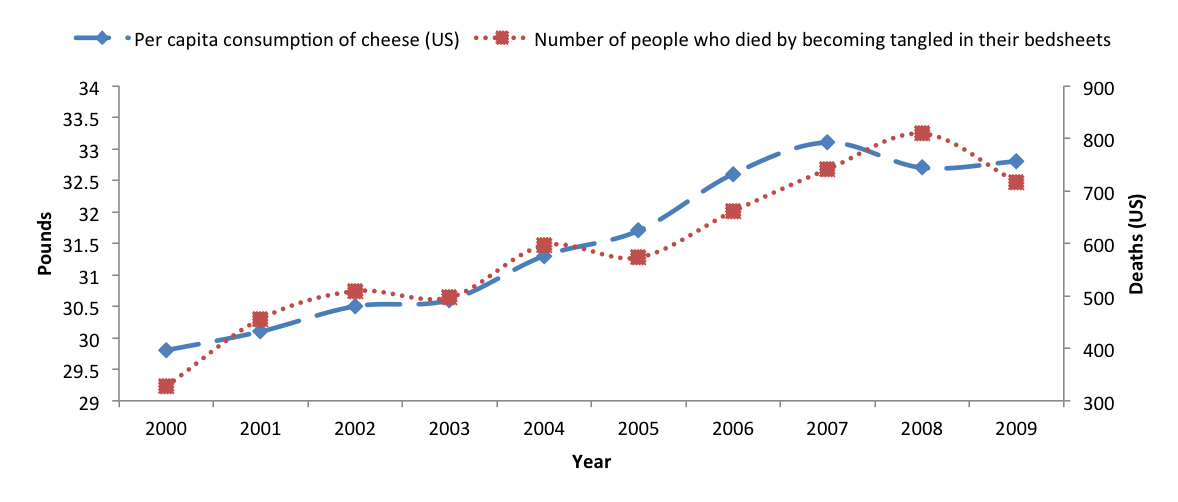
Correlation = 0.95!!
Common fallacies #
Fallacy 1: a small correlation
- wrong!
- Independence implies zero correlation BUT
- A correlation of zero does not always mean independence.
- See example 1 below.
Fallacy 2: marginal distributions and their correlation matrix uniquely determine the joint distribution.
- This is true only for elliptical families (including multivariate normal), but wrong in general!
- See example 2 below.
Example 1 #
Company’s two risks
- Let
- Consider:
This example can be made more realistic
Example 2 #
Marginals and correlations—not enough to completely determine joint distribution
Consider the following example:
- Marginals: Gamma
- Correlation:
- Different dependence structures: Normal copula vs Cook-Johnson copula
- More generally, check the
Copulatheque
Example 2 illustration: Normal vs Cook-Johnson copulas #
Copula theory #
What is a copula? #
Sklar’s representation theorem #
The copula couples, links, or connects the joint distribution to its marginals.
Sklar (1959): There exists a copula function
Under certain conditions, the copula
is unique, where
Note:
- This is one way of constructing copulas.
- These are called implicit copulas.
- Elliptical copulas are a prominent example (e.g., Gaussian copula)
Example #
Let
Finally,
- Independence copula is
- The copula captures the dependence structure, while separating the effects of the marginals (which are behind probabilities
- Other copulas generally contain parameter(s) to fine-tune
the (strength of) dependence.
When is
For
Corresponding heuristics are:
- If the event on one variable is impossible, then the joint probability is impossible.
- If the event on one variable is certain, then the joint probability boils down to the marginal of the other one.
- There cannot be negative probabilities.
We will now generalise this to
A function
- right-continuous;
- rectangle inequality holds: for all
where
A copula
Properties of a multivariate copula:
- the rectangle inequality leads us to
for all
Heuristics are the same as before.
Density associated with a copula #
For continuous marginals with respective pdf
where the copula density
Note:
- The copula
- If independent,
Example #
Let
Derive its associated density
Survival copulas #
What if we want to work with (model) survival functions
In the bivariate case, this yields
Invariance property #
- Suppose random vector
- The random vector defined by
Proof: see Theorem 2.4.3 (p. 25) of Nelsen (1999) - The usefulness of this property can be illustrated in many ways. If you have a copula describing joint distribution of insurance losses of various types, and you decide the quantity of interest is a transformation (e.g. logarithm) of these losses, then the multivariate distribution structure does not change.
- The copula is then also invariant to inflation.
- Only the marginal distributions change.
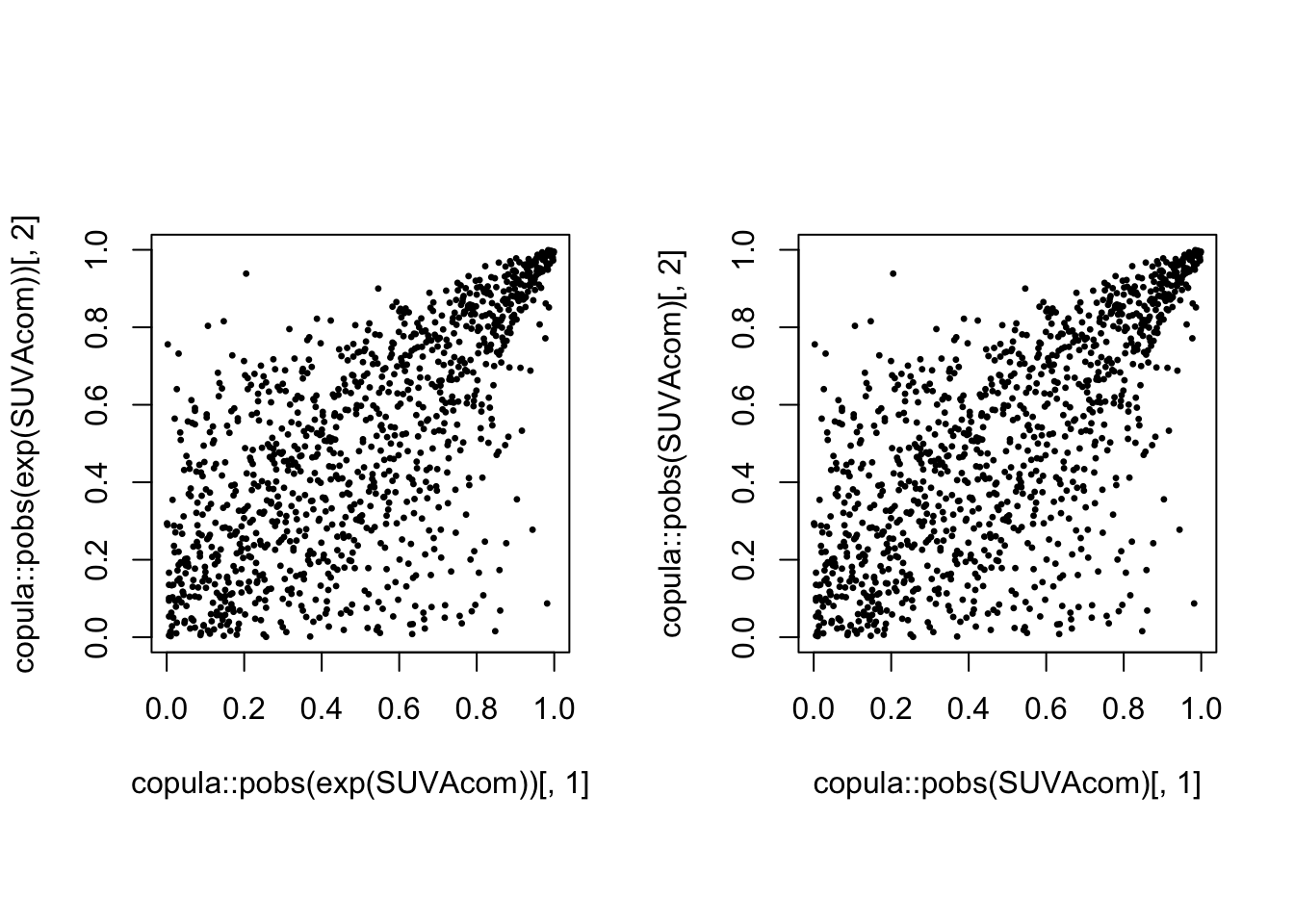
Empirical copula of the 1089 common claims (LHS) and of their log (RHS):
par(mfrow = c(1, 2), pty = "s")
plot(copula::pobs(exp(SUVAcom))[, 1], copula::pobs(exp(SUVAcom))[,
2], pch = 20, cex = 0.5)
plot(copula::pobs(SUVAcom)[, 1], copula::pobs(SUVAcom)[, 2],
pch = 20, cex = 0.5)
Main bivariate copulas #
The Fréchet bounds #
Define the Fréchet bounds as:
- Fréchet lower bound:
- Fréchet upper bound:
Any copula function satisfies the following bounds:
The Fréchet upper bound satisfies the definition of a copula, but the
Fréchet lower bound does not for dimensions
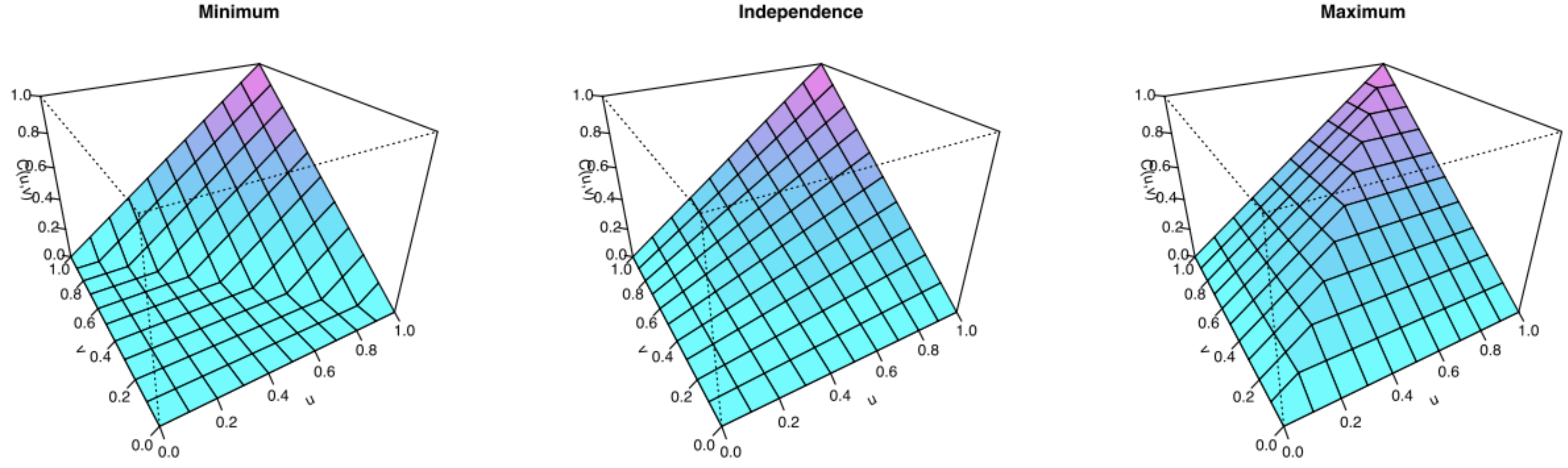
Source: Wikipedia (2020)
The Normal (aka Gaussian) copula #
Recall that
Now define its joint distribution by
Illustration of the Gaussian copula:
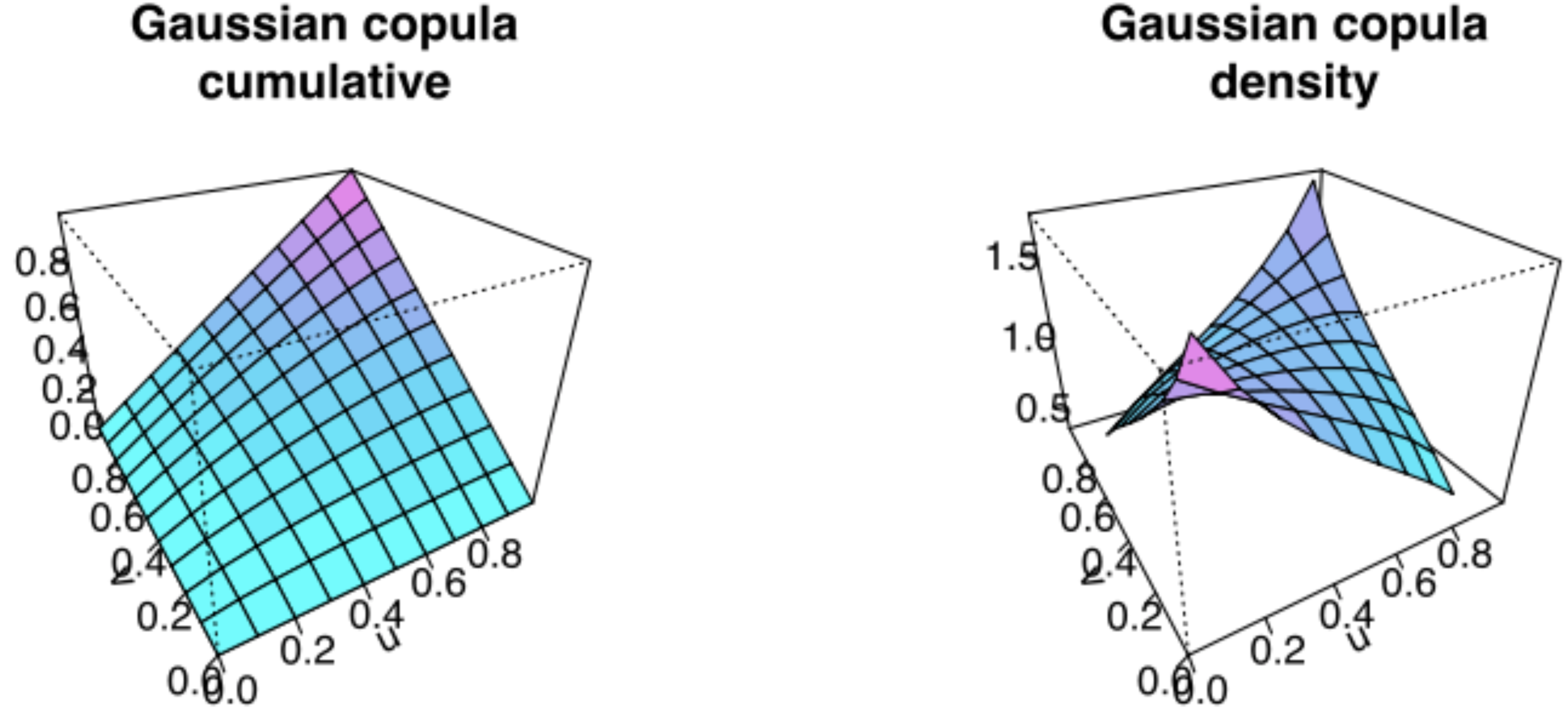
Here
The
A r vector
Now define its joint distribution by
Archimedean copulas #
for all
The Clayton copula #
The Clayton copula is defined by
It is of Archimedean type with:
Note the correspondance with Kendall’s
The Clayton copula for
We have
With parameter

With parameter

The Frank copula #
The Frank copula is defined by
Note the correspondance with Kendall’s
With parameter
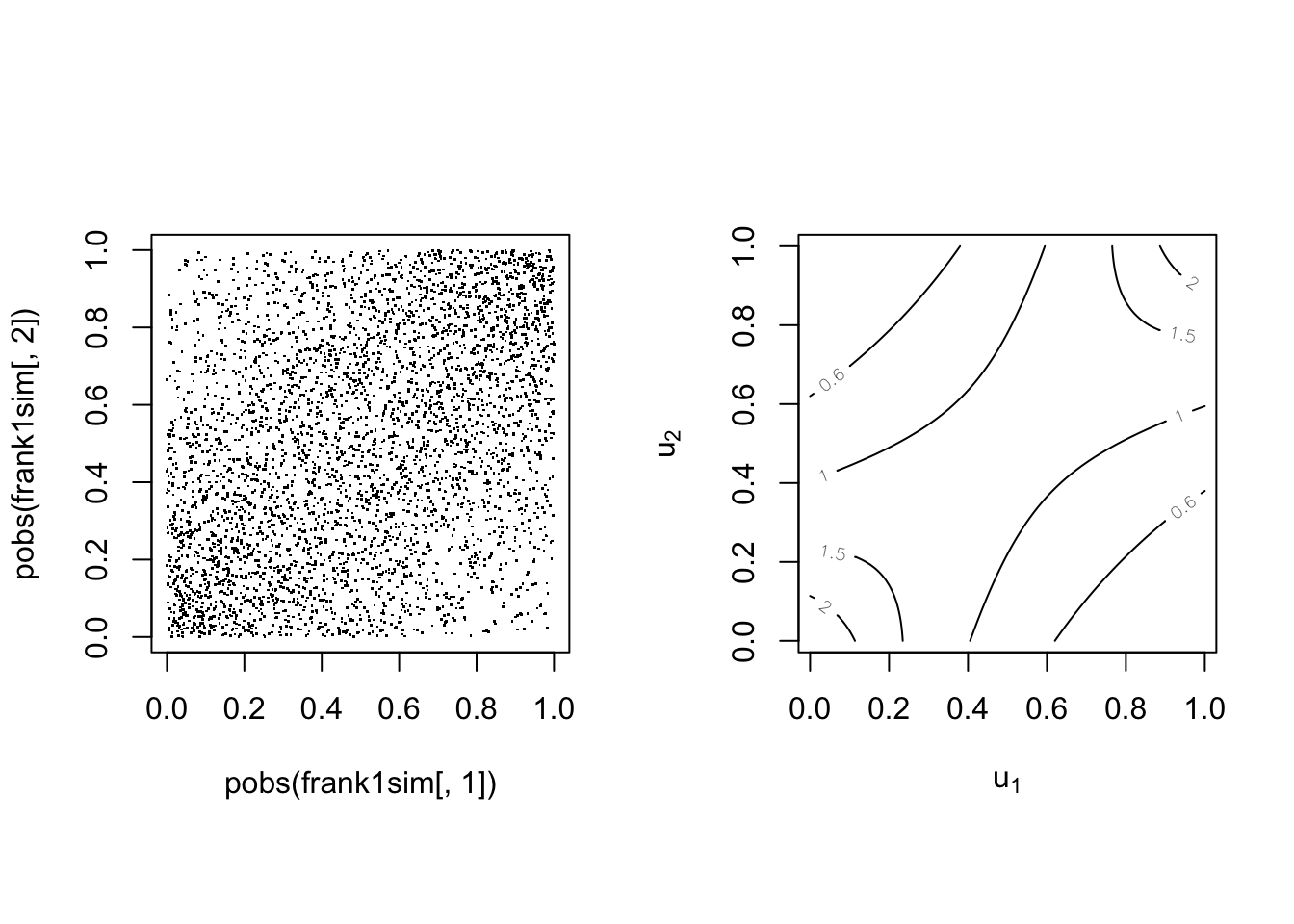
With parameter

The Gumbel(-Hougard) copula #
The Gumbel copula is defined by
Note correspondance with Kendall’s
common underlying cause.
With parameter
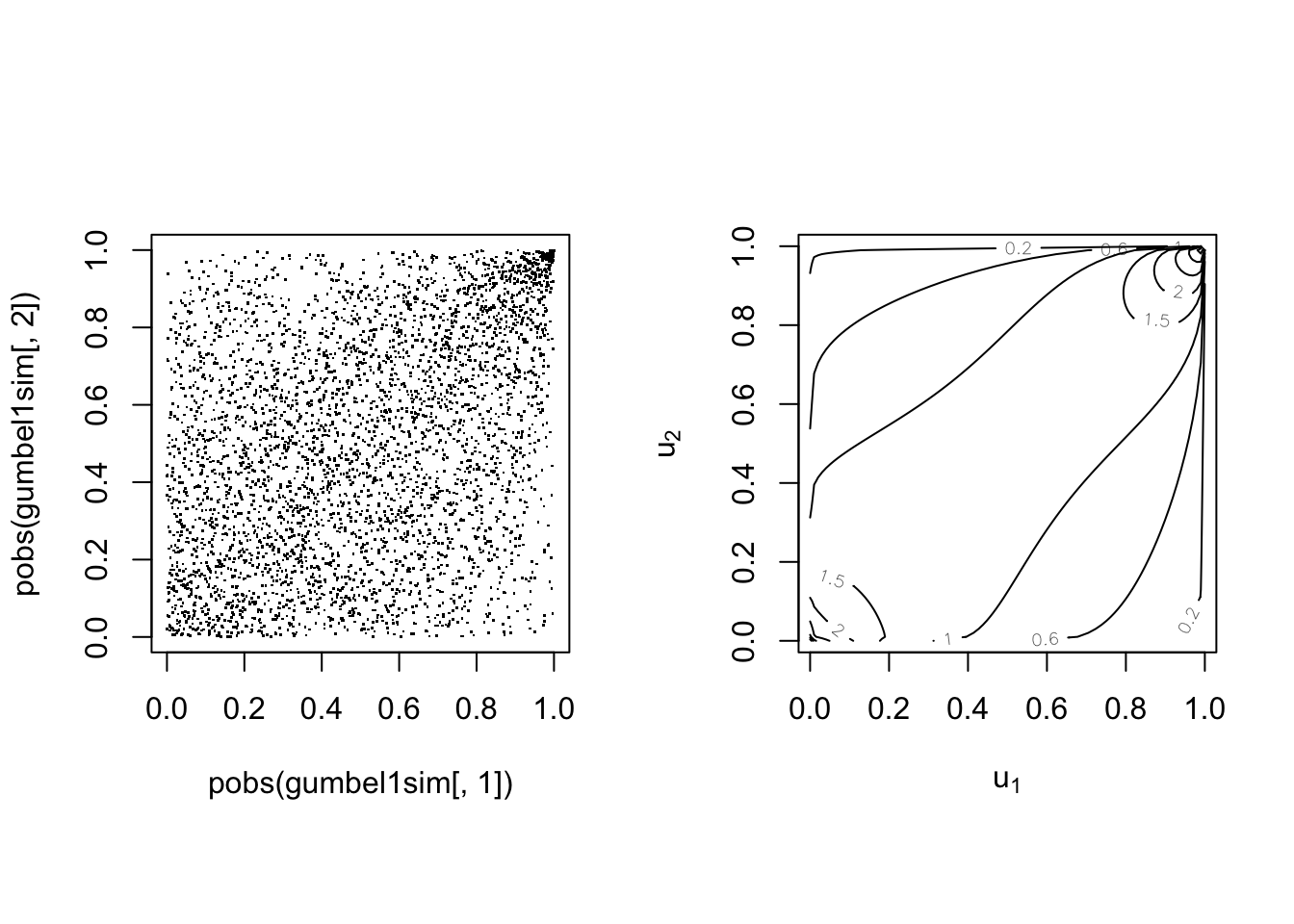
With parameter
Copula models in R #
The VineCopula package
#
- The
VineCopulapackage caters for many of the basic copula modelling requirements. - Vine copulas (Kurowicka and Joe 2011) allow for the construction of multivariate copulas with flexible dependence structures; they are outside the scope of this Module.
- The package, however, has a series of modelling functions specifically designed for bivariate copula modelling via the “BiCop-family”.
BiCop: Creates a bivariate copula by specifying the family and parameters (or Kendall’s tau). Returns an object of classBiCop.The class has the following methods:print,summary: a brief or comprehensive overview of the bivariate copula, respectively.plot,contour: surface/perspective and contour plots of the copula density. Possibly coupled with standard normal margins (default for contour).
- For most functions, you can provide an object of class
BiCopinstead of specifyingfamily,parandpar2manually.
Bivariate copulas in VineCopula
#
The following bivariate copulas are available in the
VineCopula package within the bicop family:
| Copula family | family |
par |
par2 |
|---|---|---|---|
| Gaussian | 1 | (-1, 1) | - |
| Student t | 2 | (-1, 1) | (2,Inf) |
| (Survival) Clayton | 3, 13 | (0, Inf) | - |
| Rotated Clayton (90° and 270°) | 23, 33 | (-Inf, 0) | - |
| (Survival) Gumbel | 4, 14 | [1, Inf) | - |
| Rotated Gumbel (90° and 270°) | 24, 34 | (-Inf, -1] | - |
| Frank | 5 | R {0} | - |
| (Survival) Joe | 6, 16 | (1, Inf) | - |
| Rotated Joe (90° and 270°) | 26, 36 | (-Inf, -1) | - |
| Copula family | family |
par |
par2 |
|---|---|---|---|
| (Survival) Clayton-Gumbel (BB1) | 7, 17 | (0, Inf) | [1, Inf) |
| Rotated Clayton-Gumbel (90° and 270°) | 27, 37 | (-Inf, 0) | (-Inf, -1] |
| (Survival) Joe-Gumbel (BB6) | 8, 18 | [1 ,Inf) | [1, Inf) |
| Rotated Joe-Gumbel (90° and 270°) | 28, 38 | (-Inf, -1] | (-Inf, -1] |
| (Survival) Joe-Clayton (BB7) | 9, 19 | [1, Inf) | (0, Inf) |
| Rotated Joe-Clayton (90° and 270°) | 29, 39 | (-Inf, -1] | (-Inf, 0) |
| (Survival) Joe-Frank (BB8) | 10, 20 | [1, Inf) | (0, 1] |
| Rotated Joe-Frank (90° and 270°) | 30, 40 | (-Inf, -1] | [-1, 0) |
| (Survival) Tawn type 1 | 104, 114 | [1, Inf) | [0, 1] |
| Rotated Tawn type 1 (90° and 270°) | 124, 134 | (-Inf, -1] | [0, 1] |
| (Survival) Tawn type 2 | 204, 214 | [1, Inf) | [0, 1] |
| Rotated Tawn type 2 (90° and 270°) | 224, 234 | (-Inf, -1] | [0, 1] |
All of these copulas are illustrated in the
copulatheque.
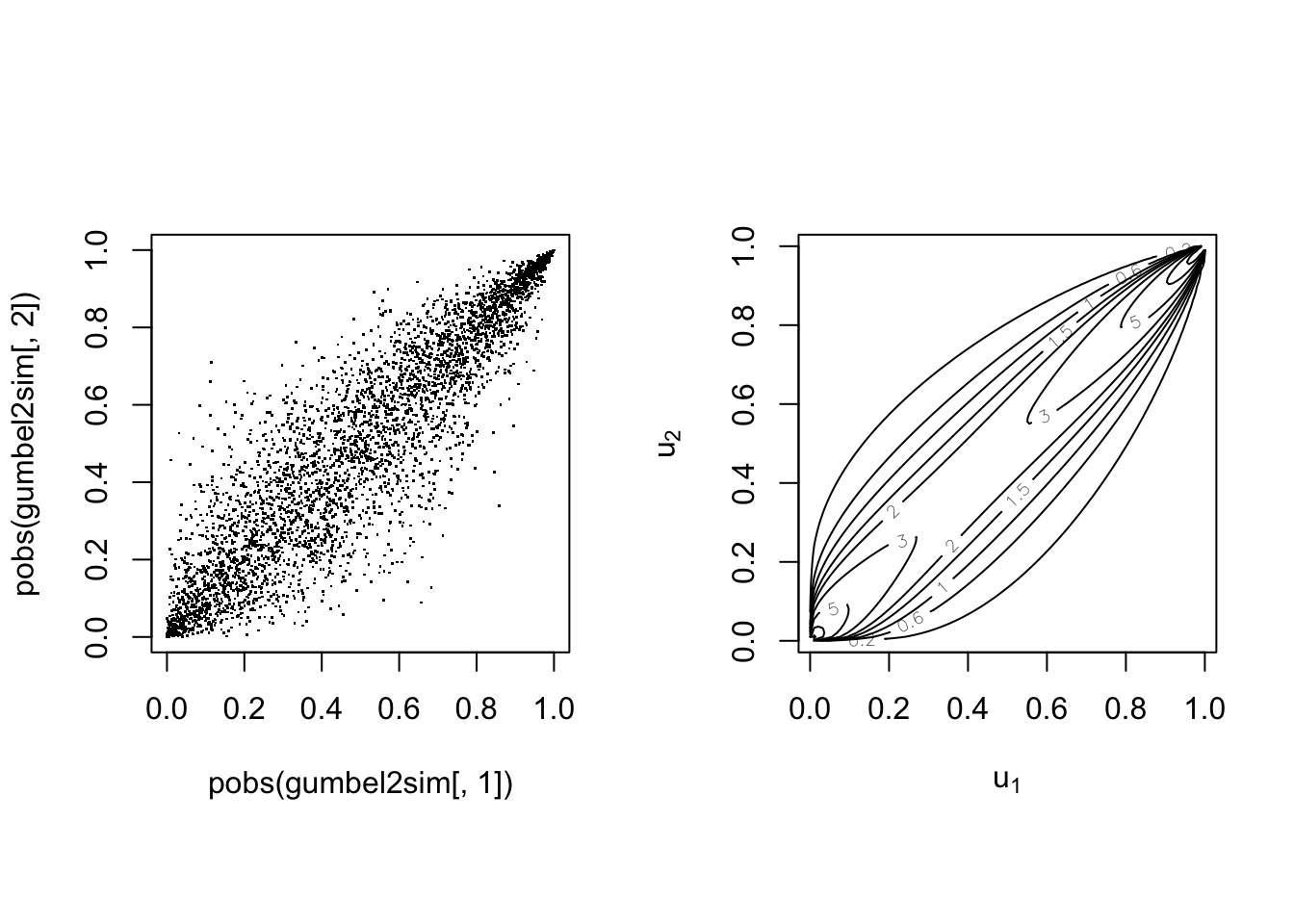
Example of Gumbel copula:
cop <- VineCopula::BiCop(4, 2)
print(cop)
## Bivariate copula: Gumbel (par = 2, tau = 0.5)
summary(cop)
## Family
## ------
## No: 4
## Name: Gumbel
##
## Parameter(s)
## ------------
## par: 2
##
## Dependence measures
## -------------------
## Kendall's tau: 0.5
## Upper TD: 0.59
## Lower TD: 0
plot(cop)
Note this is for uniform margins.
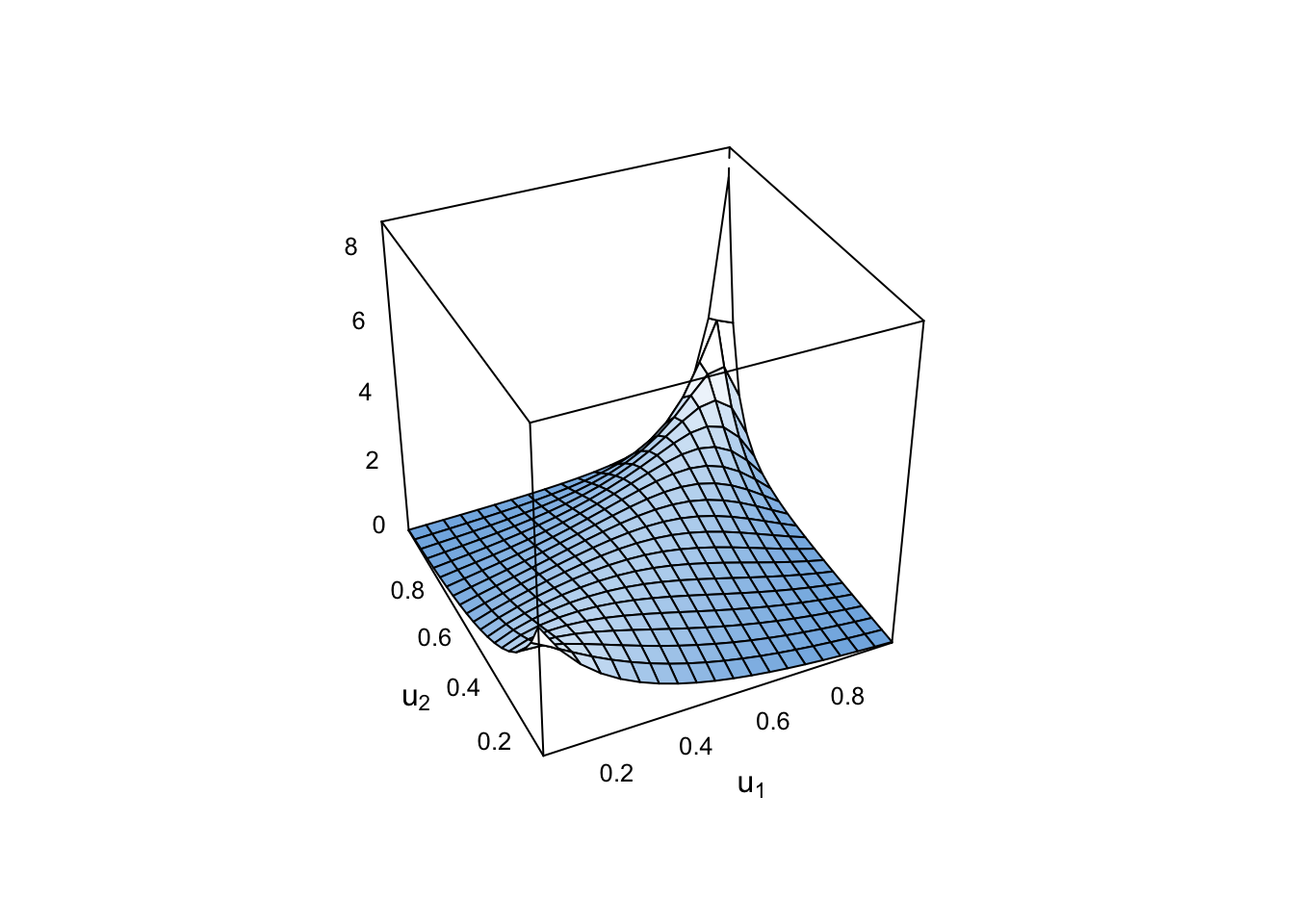
Now with a standard normal margin:
plot(cop, type = "surface", margins = "norm")

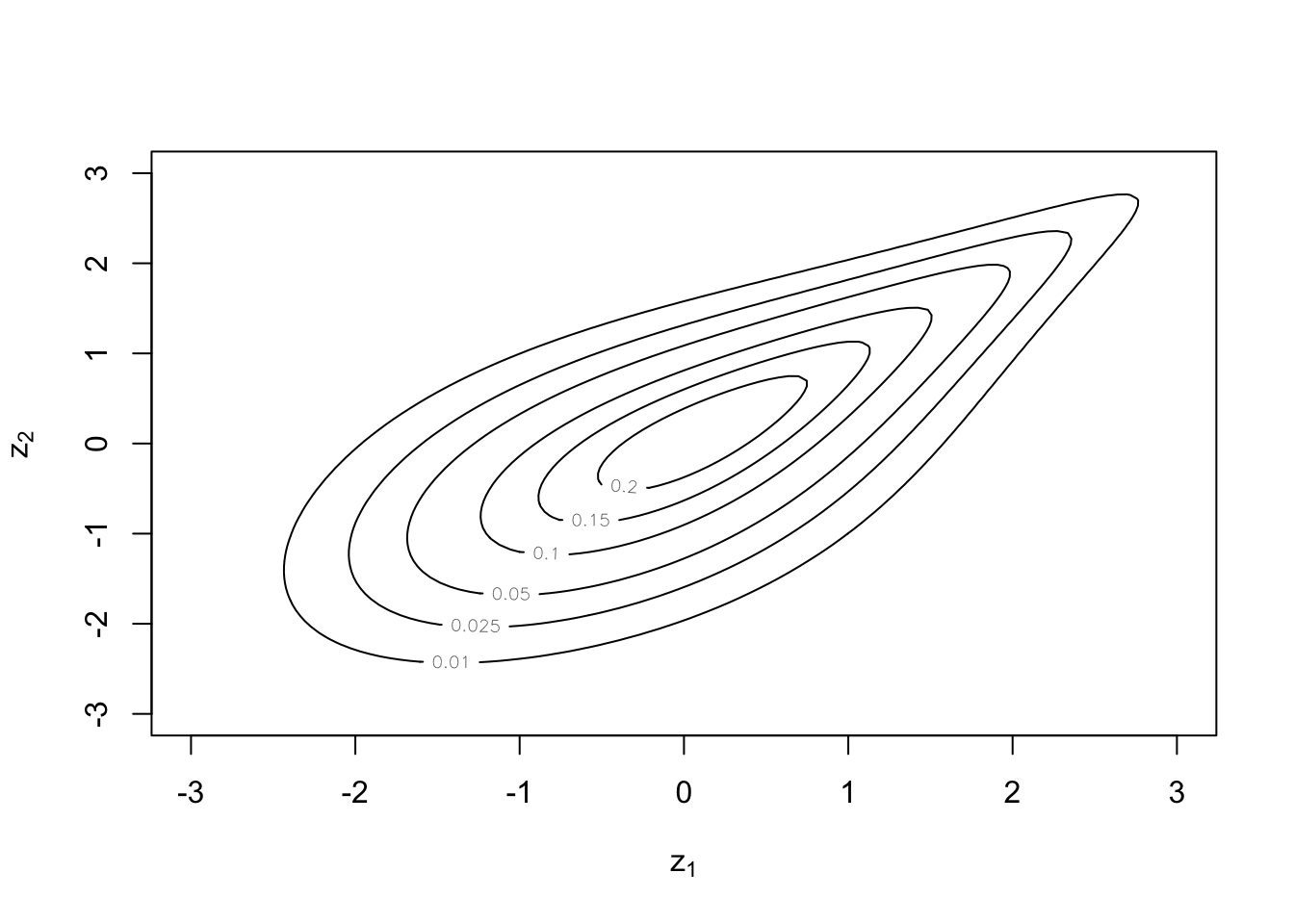
Contour plots are done with normal margins as standard:
plot(cop, type = "contour")
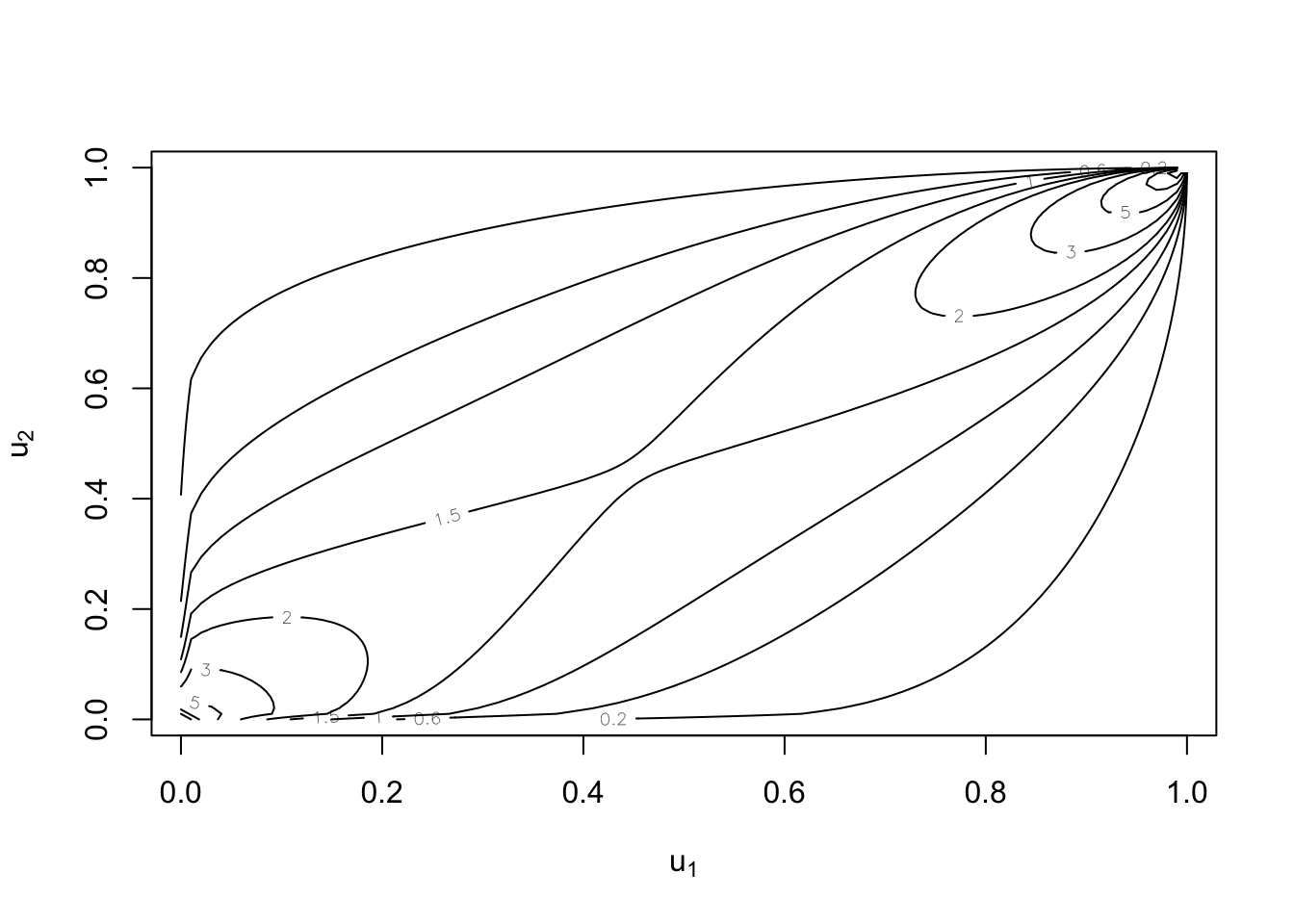
But uniform margins are still possible:
plot(cop, type = "contour", margins = "unif")
And so are exponential margins in both cases:
plot(cop, type = "contour", margins = "exp")
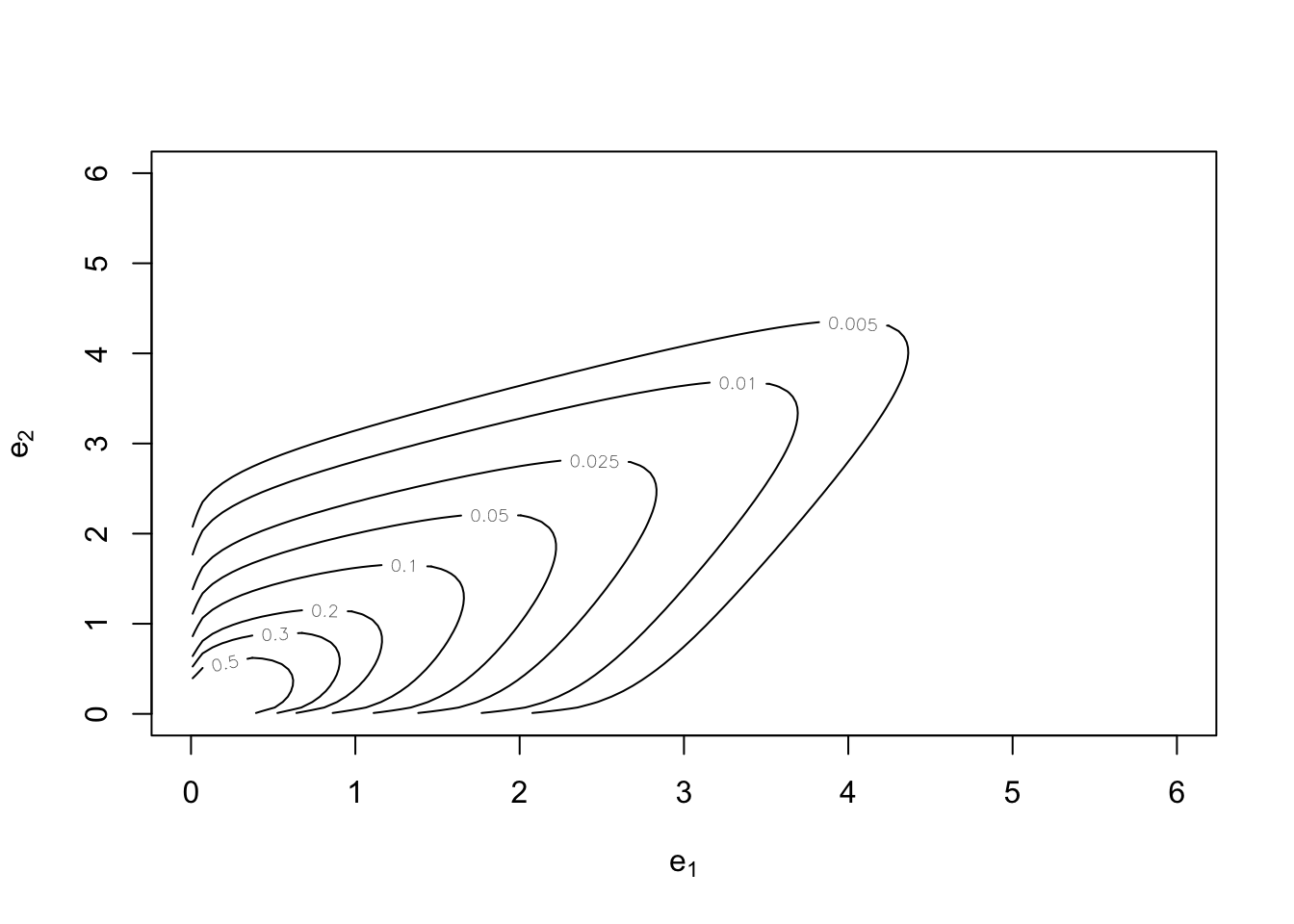
Conversion between dependence measures and parameters (for a given family): #
BiCopPar2Tau: computes the theoretical Kendall’s tau value of a bivariate copula for given parameter values.BiCopTau2Par: computes the parameter of a (one parameter) bivariate copula for a given value of Kendall’s tau.
Example of conversion for Clayton:
tau <- BiCopPar2Tau(3, 2.5)
tau
## [1] 0.5555556
theta <- 2 * tau/(1 - tau)
theta
## [1] 2.5
BiCopTau2Par(3, tau)
## [1] 2.5
Evaluate functions related to a bivariate copula: #
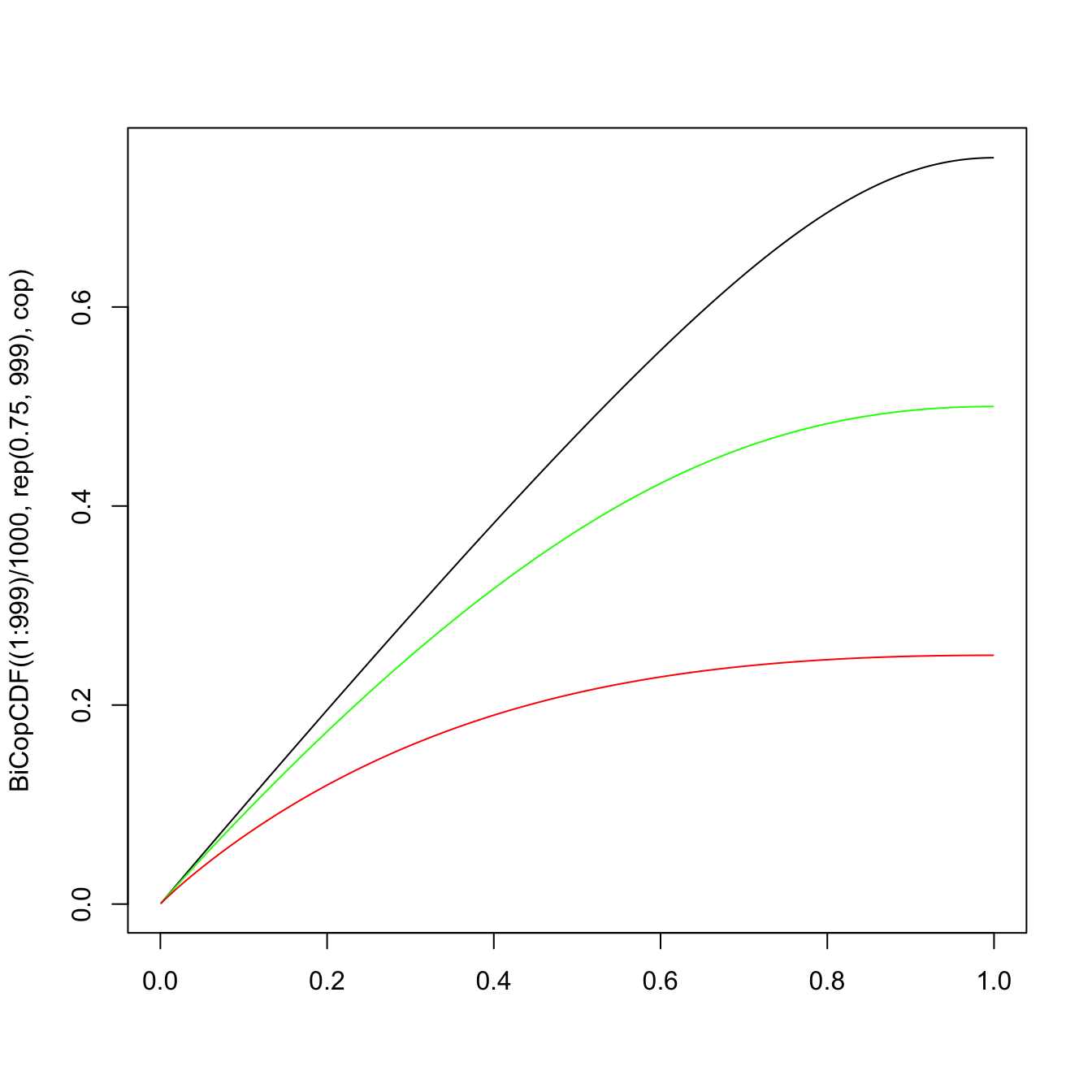
BiCopPDF/BiCopCDF: evaluates the pdf/cdf of a given parametric bivariate copula.BiCopDeriv: evaluates the derivative of a given parametric bivariate copula density with respect to its parameter(s) or one of its arguments.
plot((1:999)/1000, BiCopCDF((1:999)/1000, rep(0.75, 999), cop),
type = "l", xlab = "") #u_2 = 0.75
lines((1:999)/1000, BiCopCDF((1:999)/1000, rep(0.5, 999), cop),
type = "l", col = "green") #u_2 = 0.5
lines((1:999)/1000, BiCopCDF((1:999)/1000, rep(0.25, 999), cop),
type = "l", col = "red") #u_2 = 0.25
- Remember that if
- This forms the basis of most simulation techniques, as a pseudo-uniform
- We will introduce the general conditional distribution method.
- The overarching idea is (for the bivariate case):
- simulate two independent uniform random variable
- “tweak”
- map
- simulate two independent uniform random variable
- However, there are some specific, more efficient algorithms that are available for certain types of copulas (see, e.g. Nelsen 1999).
- In R, the function
BiCopSimwill simulate from a given parametric bivariate copula.
For the “tweak”, we will need the conditional distribution function for
In particular, we will need its inverse.
For the copula
For copulas of the BiCop family:
BiCopHfunc: evaluates the conditional distribution functionBiCopHinv: evaluates the inverse conditional distribution functionBiCopHfuncDeriv: evaluates the derivative of a given conditional parametric bivariate copula (h-function) with respect to its parameter(s) or one of its arguments.
Goal: generate a pair of pseudo-random variables
Algorithm
- Generate two independent uniform
- Set
- Map
Let
Use of the conditional distribution method yields
- We can use the uniforms given in the question such that
- Set
- Mapping
The following algorithms are provided for illustration purposes. They are not assessable.
Let
The following algorithm generates
- construct the lower triangular matrix
- generate a column vector of independent standard Normal rv’s
- take the matrix product of
- set
- set
Let
- generate a column vector of independent
- generate
- set
- set
We simulate 4000 pairs
Simul.u <- BiCopSim(4000, cop)
head(Simul.u, 15)
## [,1] [,2]
## [1,] 0.50867346 0.3359880
## [2,] 0.39195033 0.2236886
## [3,] 0.41313775 0.4327339
## [4,] 0.49581195 0.2732273
## [5,] 0.06705059 0.1024408
## [6,] 0.69906709 0.7715066
## [7,] 0.20296035 0.2651919
## [8,] 0.97195829 0.9397084
## [9,] 0.61523236 0.8601095
## [10,] 0.63954756 0.3616802
## [11,] 0.15976695 0.2685132
## [12,] 0.23797290 0.2928241
## [13,] 0.76436559 0.8817227
## [14,] 0.08886271 0.2835281
## [15,] 0.87892913 0.5255004
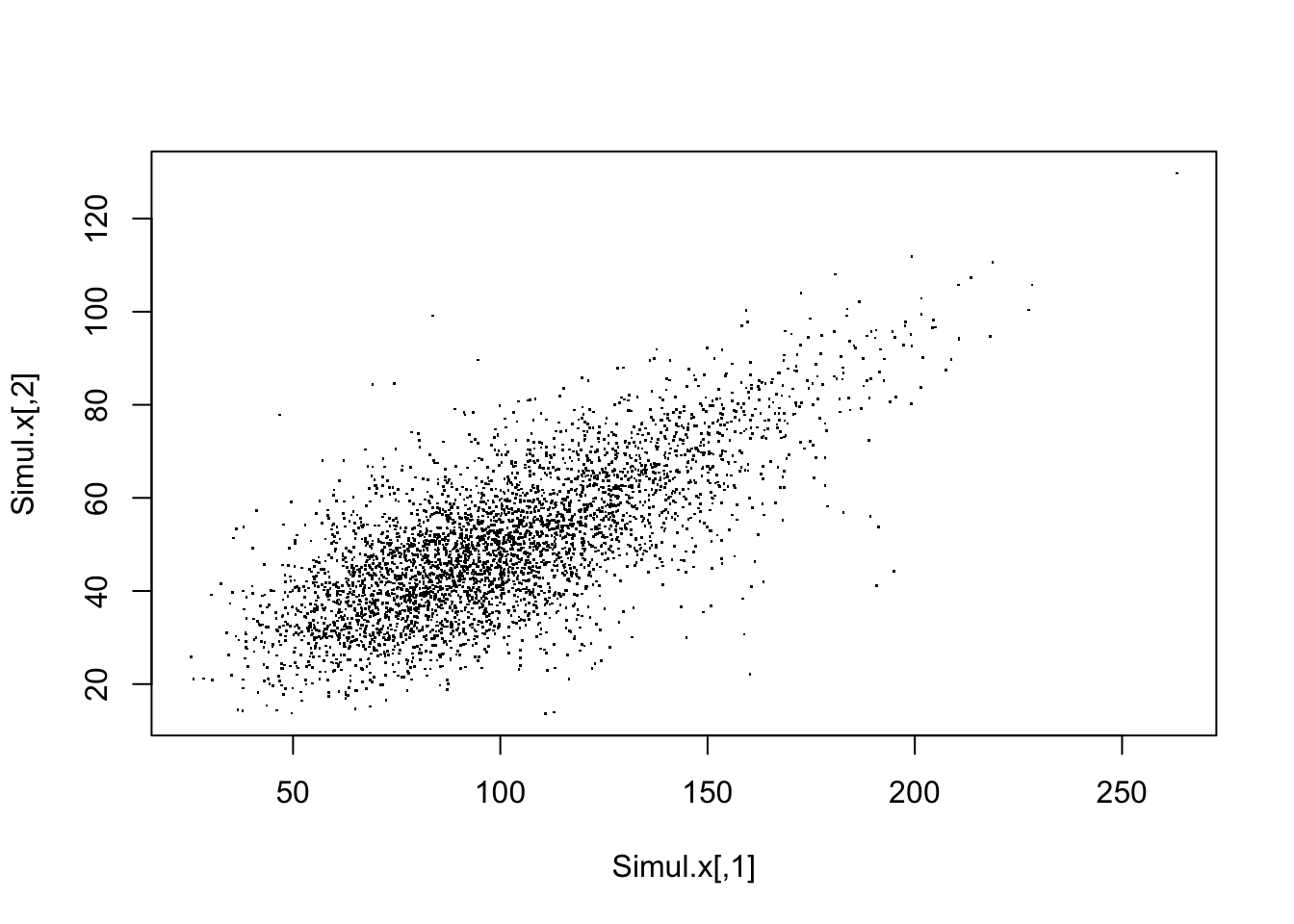
We then need to map them into the correct margins, say two gammas of shape parameter 10 and mean 100 and 50, respectively:
Simul.x <- cbind(qgamma(Simul.u[, 1], 10, 0.1), qgamma(Simul.u[,
2], 10, 0.2))
head(Simul.x, 15)
## [,1] [,2]
## [1,] 97.36284 42.07389
## [2,] 88.43264 37.50420
## [3,] 90.04144 45.76470
## [4,] 96.36203 39.58887
## [5,] 57.37719 31.26507
## [6,] 113.78008 60.81192
## [7,] 73.16214 39.26006
## [8,] 168.62815 76.57093
## [9,] 106.05850 67.09440
## [10,] 108.19177 43.06246
## [11,] 69.02607 39.39634
## [12,] 76.24157 40.37899
## [13,] 120.78114 69.09224
## [14,] 60.70501 40.00614
## [15,] 137.63631 49.34196
plot(Simul.x, pch = ".")
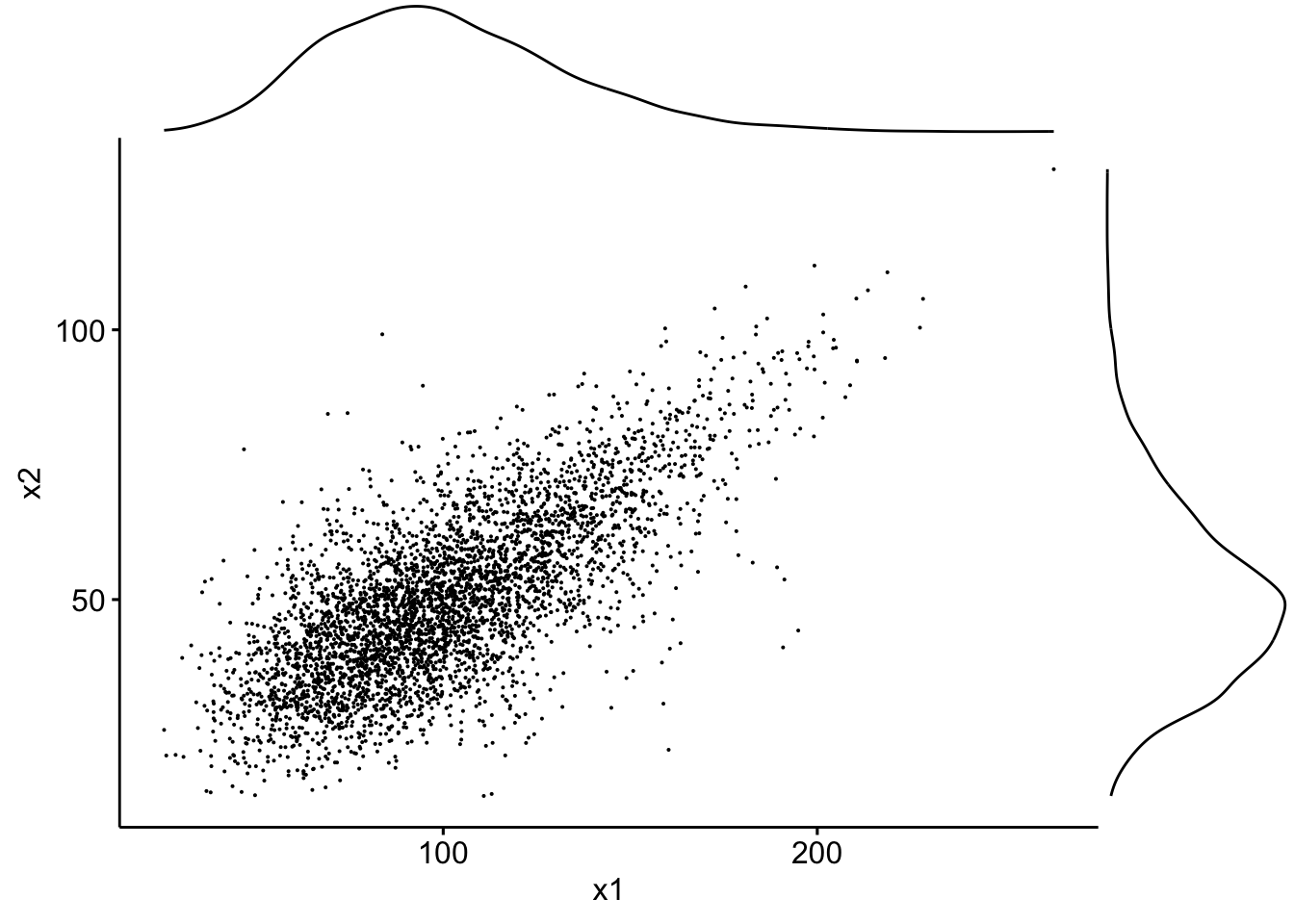
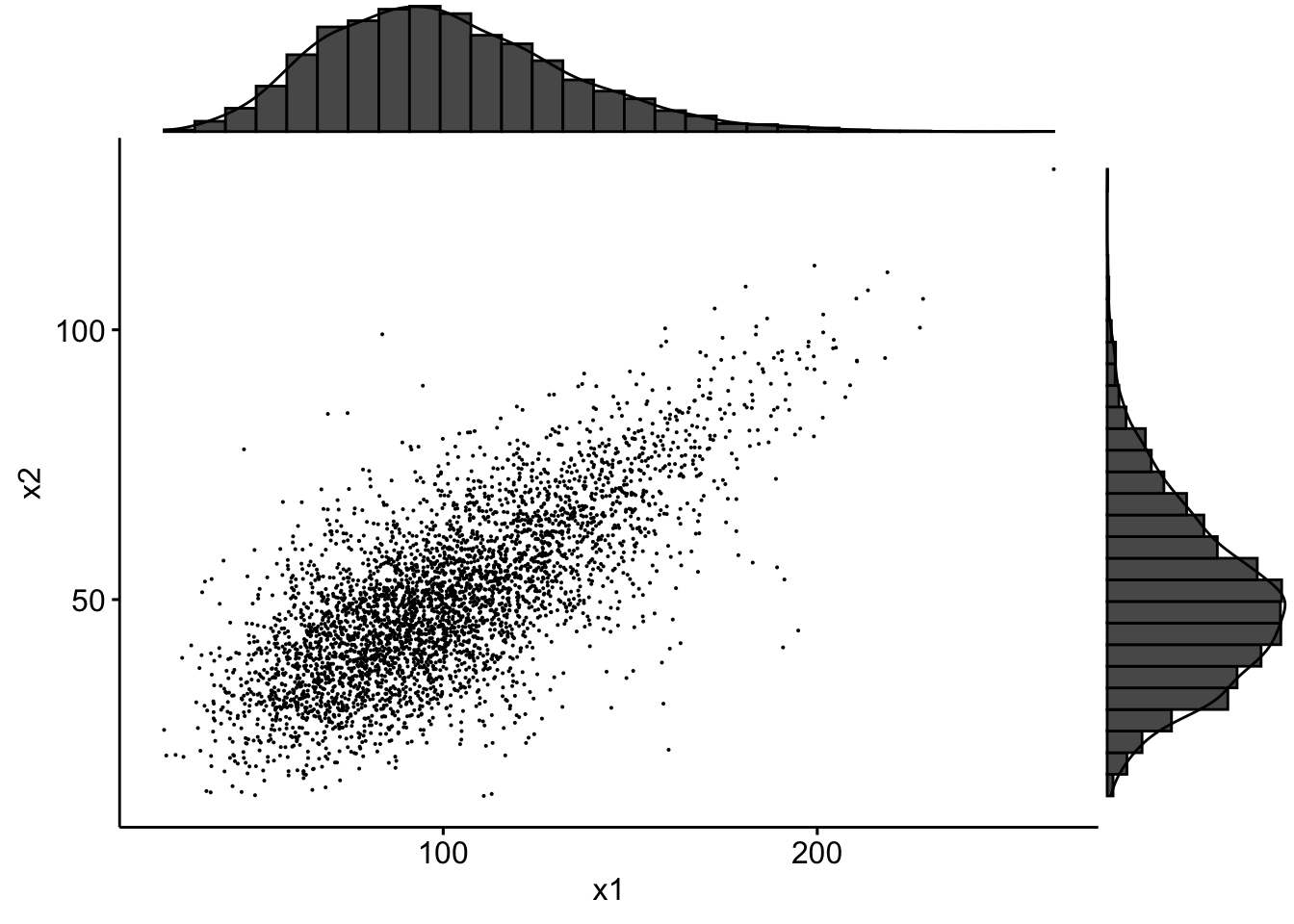
If we use the packages ggplot2, ggpubr and ggExtra one can superimpose density plots:
data <- tibble(x1 = Simul.x[, 1], x2 = Simul.x[, 2])
sp <- ggscatter(data, x = "x1", y = "x2", size = 0.05)
ggMarginal(sp, type = "density")
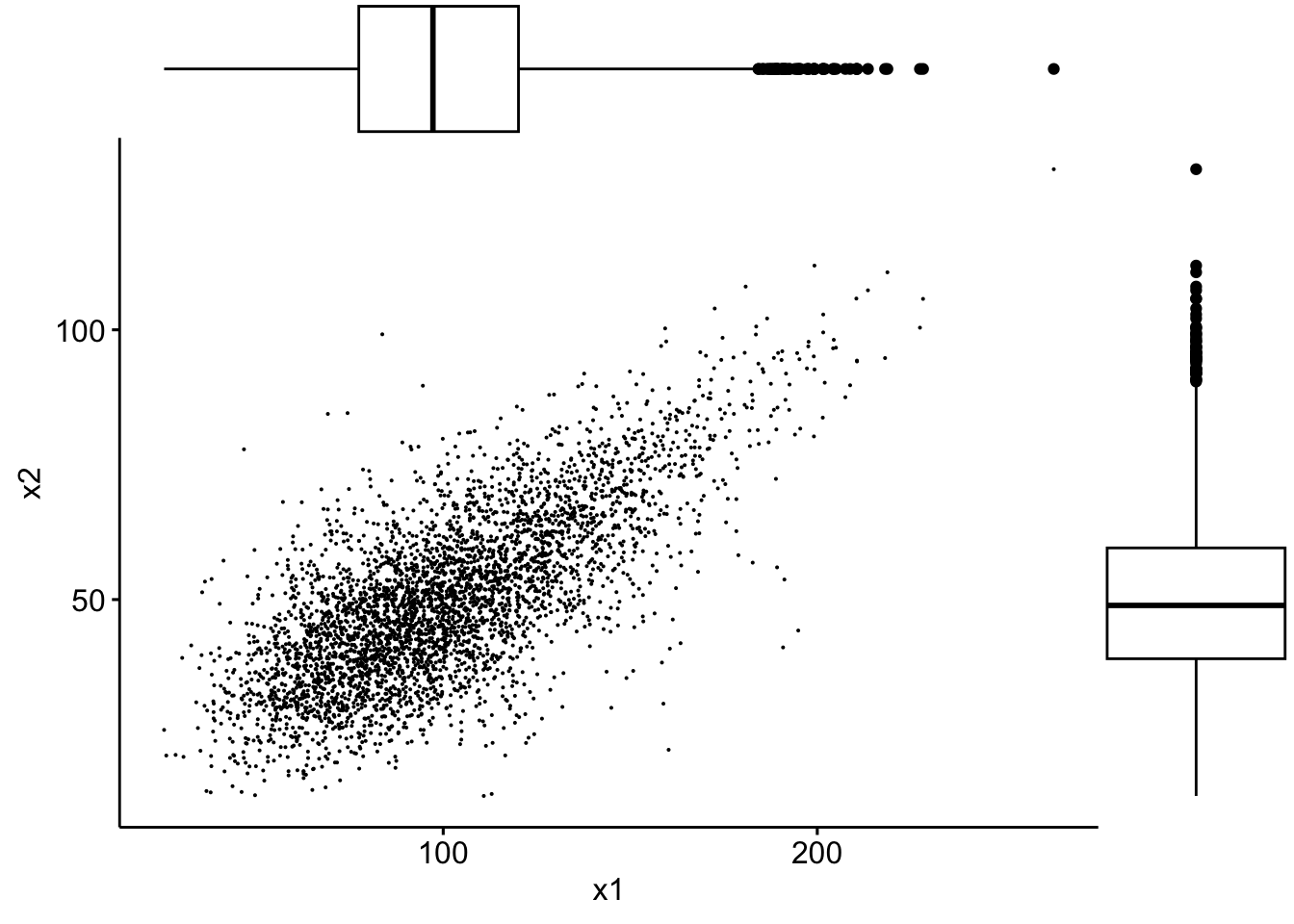
… or boxplots:
sp2 <- ggscatter(data, x = "x1", y = "x2", size = 0.05)
ggMarginal(sp2, type = "boxplot")
… or violin plots:
sp3 <- ggscatter(data, x = "x1", y = "x2", size = 0.05)
ggMarginal(sp3, type = "violin")

… or densigram plots:
sp4 <- ggscatter(data, x = "x1", y = "x2", size = 0.05)
ggMarginal(sp4, type = "densigram")
## Warning: The dot-dot notation (`..density..`) was deprecated in ggplot2 3.4.0.
## ℹ Please use `after_stat(density)` instead.
## ℹ The deprecated feature was likely used in the ggExtra package.
## Please report the issue at
## <https://github.com/daattali/ggExtra/issues>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning
## was generated.
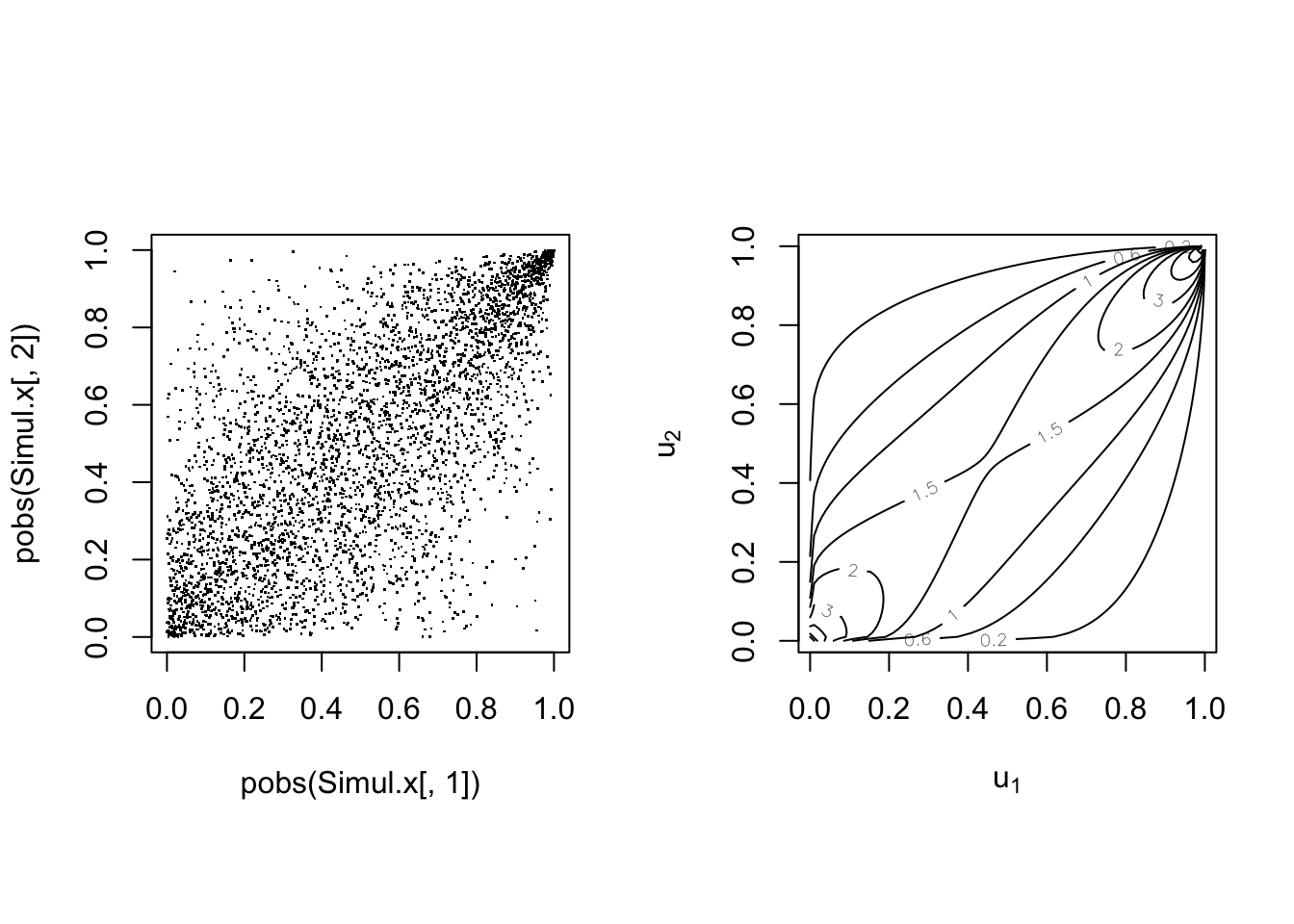
par(mfrow = c(1, 2), pty = "s")
plot(pobs(Simul.x[, 1]), pobs(Simul.x[, 2]), pch = ".")
plot(cop, type = "contour", margins = "unif")
data2 <- tibble(x1 = pobs(Simul.x[, 1]), x2 = pobs(Simul.x[,
2]))
sp3 <- ggscatter(data2, x = "x1", y = "x2", size = 0.05)
ggMarginal(sp3, type = "densigram")
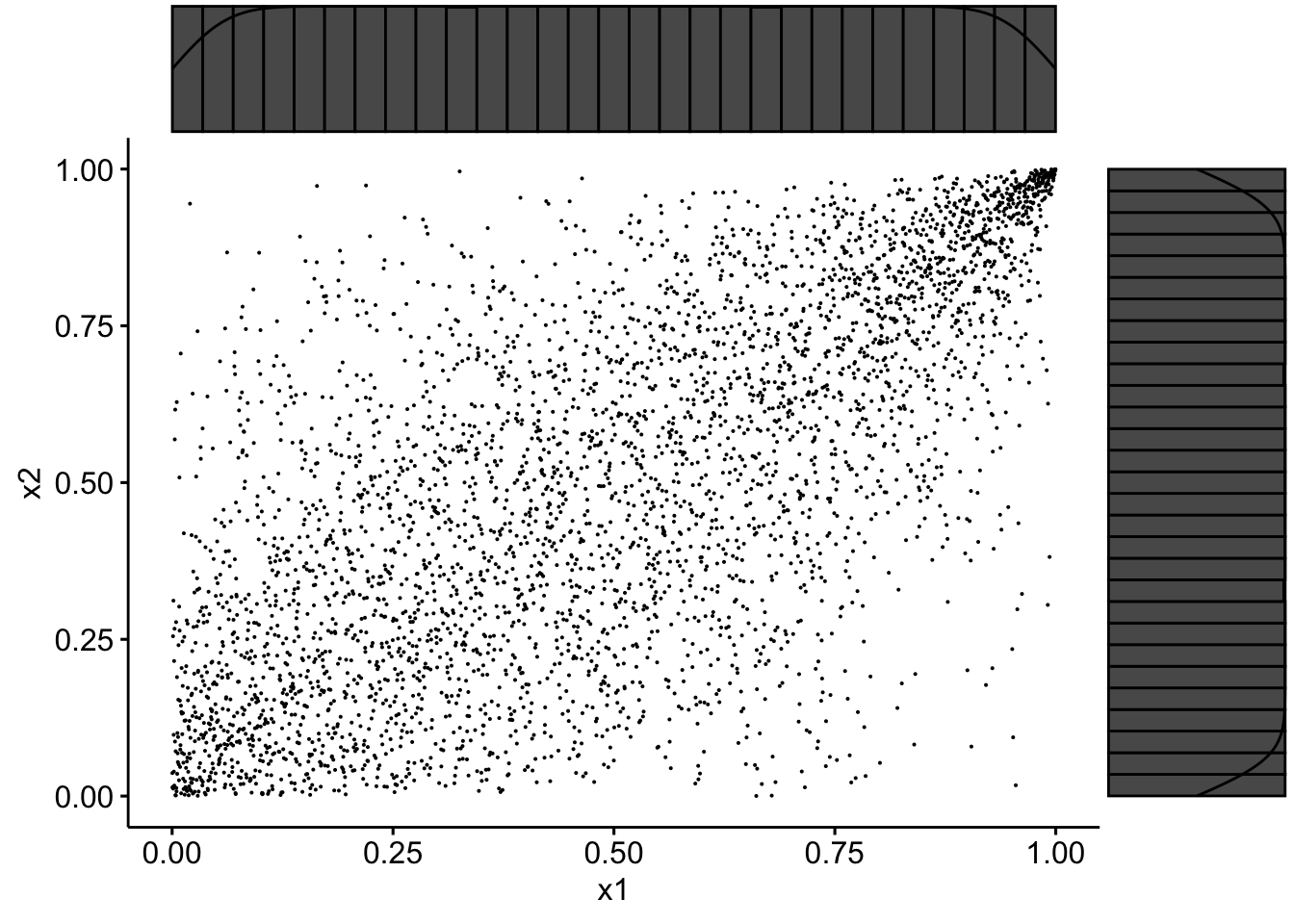
Ranks have uniform margins as expected.
The
VineCopula package offers many functions for fitting copulas:
BiCopKDE: A kernel density estimate of the copula density is visualised.BiCopSelect: Estimates the parameters of a bivariate copula for a set of families and selects the best fitting model (using either AIC or BIC). Returns an object of classBiCop.BiCopEst: Estimates parameters of a bivariate copula with a prespecified family. Returns an object of classBiCop. Estimation can be done by- maximum likelihood (method = “mle”) or
- inversion of the empirical Kendall’s tau (method = “itau”, only available for one-parameter families).
BiCopGofTest: Goodness-of-Fit tests for bivariate copulas.
VineCopula: SUVA data
#
BiCopKDE(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]))

BiCopKDE(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), margins = "unif")

SUVAselect <- BiCopSelect(pobs(SUVAcom[, 1]), pobs(SUVAcom[,
2]), selectioncrit = "BIC")
summary(SUVAselect)
## Family
## ------
## No: 10
## Name: BB8
##
## Parameter(s)
## ------------
## par: 3.08
## par2: 0.99
## Dependence measures
## -------------------
## Kendall's tau: 0.52 (empirical = 0.52, p value < 0.01)
## Upper TD: 0
## Lower TD: 0
##
## Fit statistics
## --------------
## logLik: 488.99
## AIC: -973.98
## BIC: -964
For comparison:
SUVAsurvClayton <- BiCopEst(pobs(SUVAcom[, 1]), pobs(SUVAcom[,
2]), family = 13)
summary(SUVAsurvClayton)
## Family
## ------
## No: 13
## Name: Survival Clayton
##
## Parameter(s)
## ------------
## par: 2.07
##
## Dependence measures
## -------------------
## Kendall's tau: 0.51 (empirical = 0.52, p value < 0.01)
## Upper TD: 0.72
## Lower TD: 0
##
## Fit statistics
## --------------
## logLik: 478.14
## AIC: -954.28
## BIC: -949.29
White’s test:
BiCopGofTest(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), SUVAselect)
## Error in BiCopGofTest(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), SUVAselect): The goodness-of-fit test based on White's information matrix equality is not implemented for the BB copulas.
BiCopGofTest(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), SUVAsurvClayton)
## $statistic
## [,1]
## [1,] 1.343252
##
## $p.value
## [1] 0.26
We cannot perform the test on the BB8 copula (R informs us that The goodness-of-fit test based on White's information matrix equality is not implemented for the BB copulas.), but also cannot reject the null on the Survival Clayton.
BiCopGofTest(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), SUVAselect,
method = "kendall")
## $p.value.CvM
## [1] 0.21
##
## $p.value.KS
## [1] 0.24
##
## $statistic.CvM
## [1] 0.08458458
##
## $statistic.KS
## [1] 0.738938
BiCopGofTest(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), SUVAsurvClayton,
method = "kendall")
## $p.value.CvM
## [1] 0.34
##
## $p.value.KS
## [1] 0.23
##
## $statistic.CvM
## [1] 0.08144334
##
## $statistic.KS
## [1] 0.7731786
par(mfrow = c(1, 2), pty = "s")
BiCopKDE(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), margins = "unif")
plot(SUVAselect, type = "contour", margins = "unif")
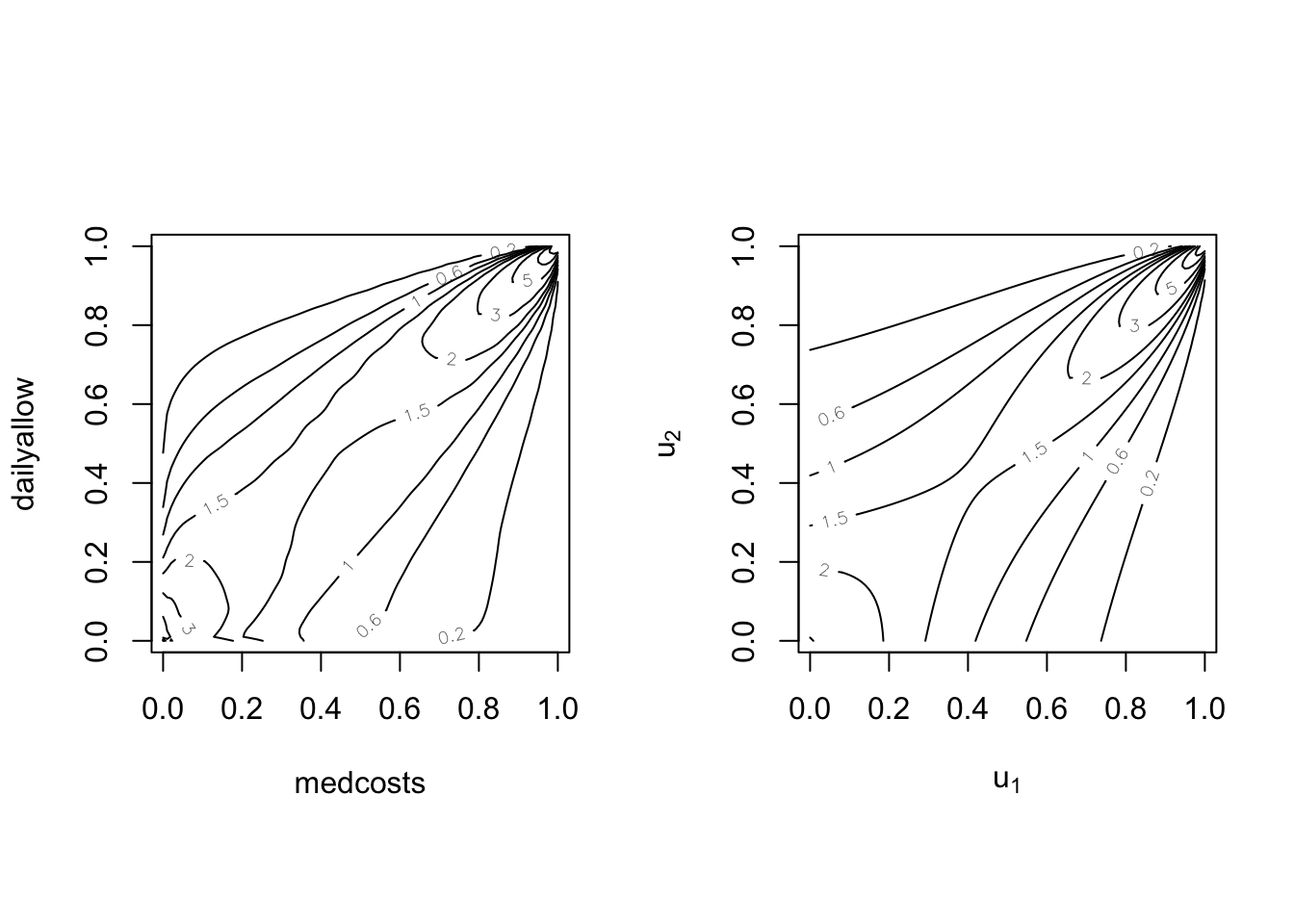
par(mfrow = c(1, 2), pty = "s")
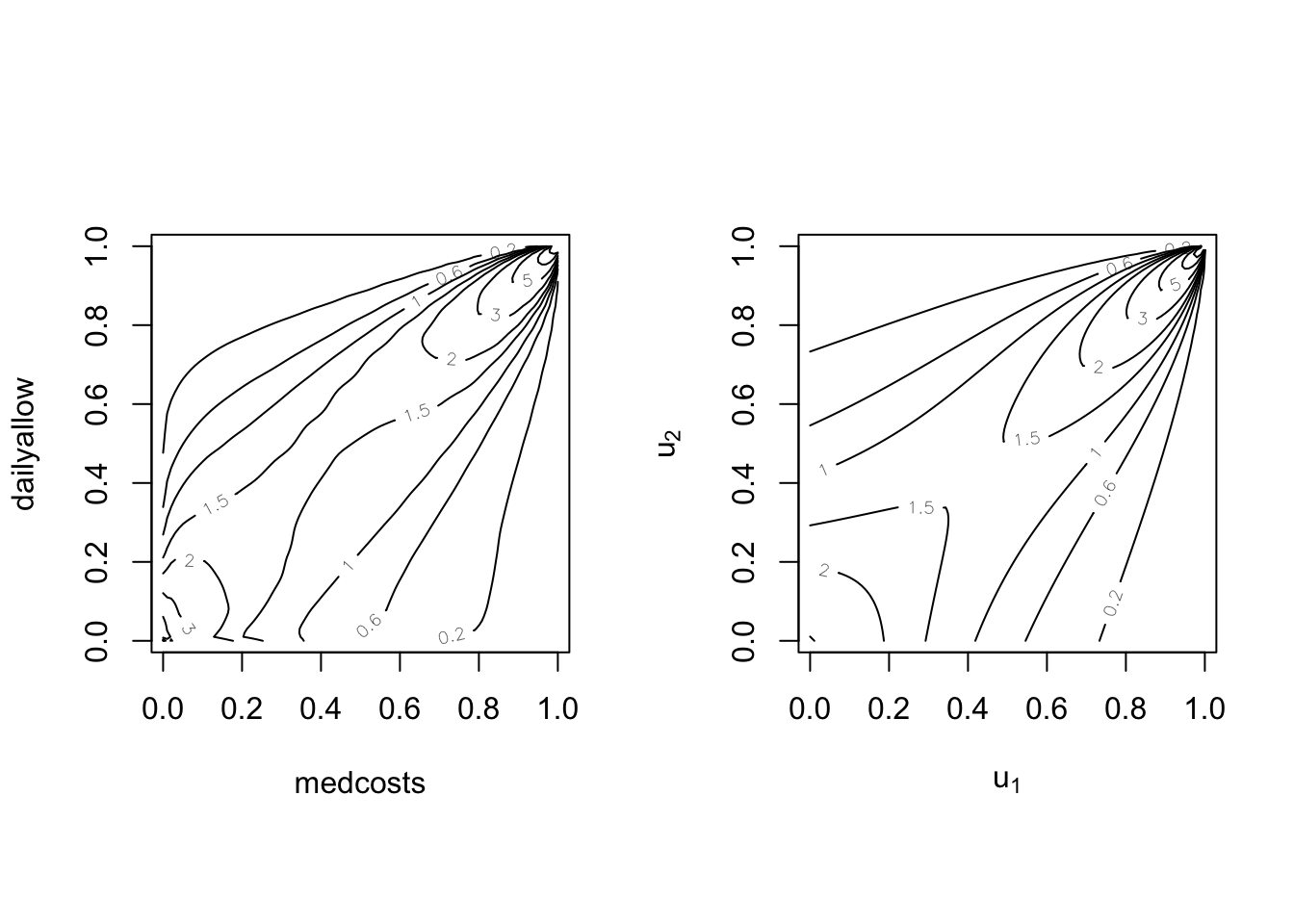
BiCopKDE(pobs(SUVAcom[, 1]), pobs(SUVAcom[, 2]), margins = "unif")
plot(SUVAsurvClayton, type = "contour", margins = "unif")
- Data consists of 1,500 general liability claims.
- Provided by the Insurance Services Office, Inc.
- Policy contains policy limits, and hence, censoring.
We will fit this data mostly “by hand” for transparency (and since we need to allow for censoring). R codes are provided separately.
Loss.ALAE <- read_csv("LossData-FV.csv")
## Rows: 1500 Columns: 4
## ── Column specification ──────────────────────────────────────────────
## Delimiter: ","
## dbl (4): LOSS, ALAE, LIMIT, CENSOR
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
as_tibble(Loss.ALAE)
## # A tibble: 1,500 × 4
## LOSS ALAE LIMIT CENSOR
## <dbl> <dbl> <dbl> <dbl>
## 1 10 3806 500000 0
## 2 24 5658 1000000 0
## 3 45 321 1000000 0
## 4 51 305 500000 0
## 5 60 758 500000 0
## 6 74 8768 2000000 0
## 7 75 1805 500000 0
## 8 78 78 500000 0
## 9 87 46534 500000 0
## 10 100 489 300000 0
## # ℹ 1,490 more rows
| Loss | ALAE | Policy Limit | Loss (Uncensored) | Loss (Censored) | |
|---|---|---|---|---|---|
| Number | 1,500 | 1,500 | 1,352 | 1,466 | 34 |
| Mean | 41,208 | 12,588 | 559,098 | 37,110 | 217,491 |
| Median | 12,000 | 5,471 | 500,000 | 11,048 | 100,000 |
| Std Deviation | 102,748 | 28,146 | 418,649 | 92,513 | 258,205 |
| Minimum | 10 | 15 | 5,000 | 10 | 5,000 |
| Maximum | 2,173,595 | 501,863 | 7,500,000 | 2,173,595 | 1,000,000 |
| 25th quantile | 4,000 | 2,333 | 300,000 | 3,750 | 50,000 |
| 75th quantile | 35,000 | 12,577 | 1,000,000 | 32,000 | 300,000 |
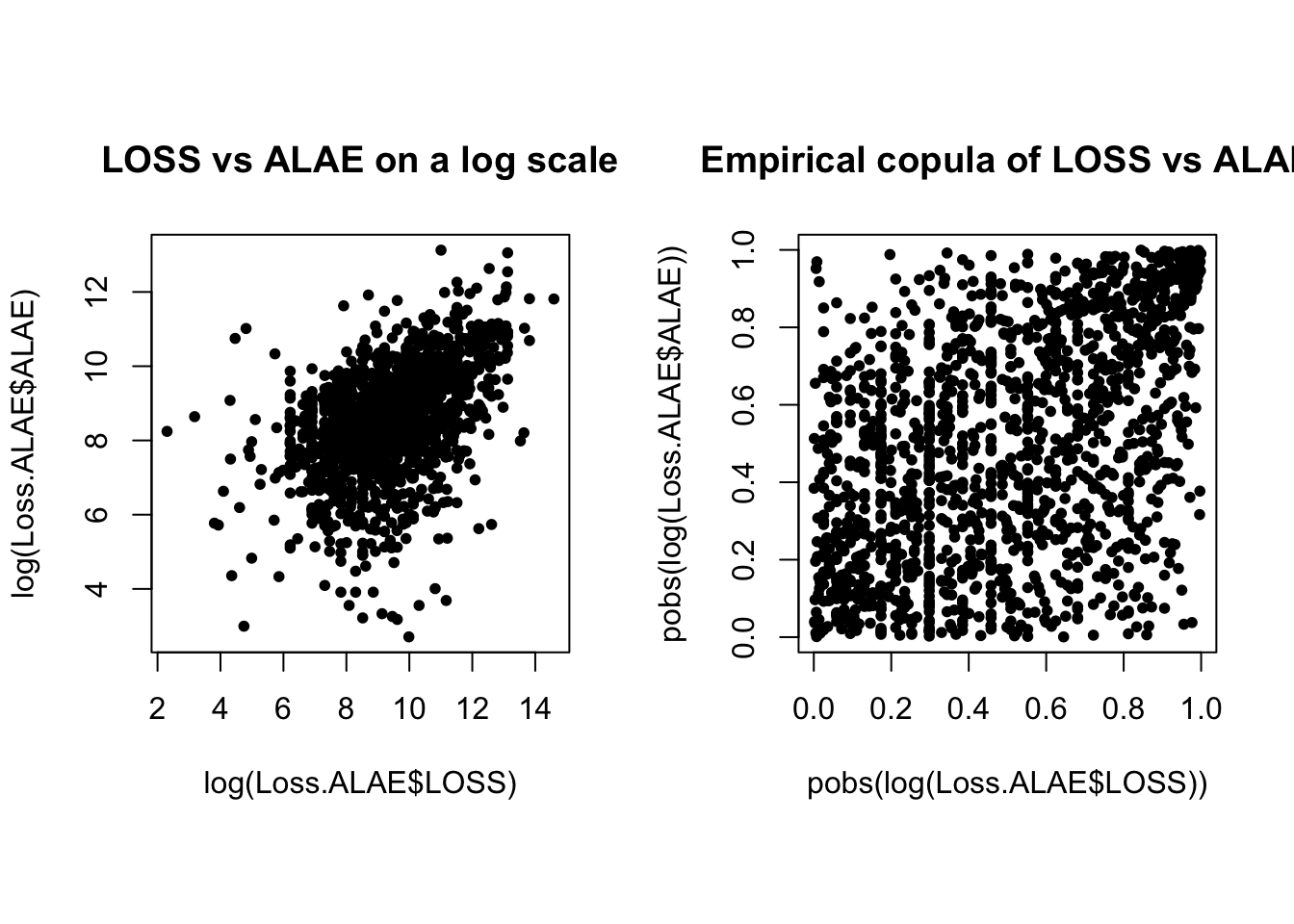
par(mfrow = c(1, 2), pty = "s")
plot(log(Loss.ALAE$LOSS), log(Loss.ALAE$ALAE), main = "LOSS vs ALAE on a log scale",
pch = 20)
plot(pobs(log(Loss.ALAE$LOSS)), pobs(log(Loss.ALAE$ALAE)), main = "Empirical copula of LOSS vs ALAE",
pch = 20)
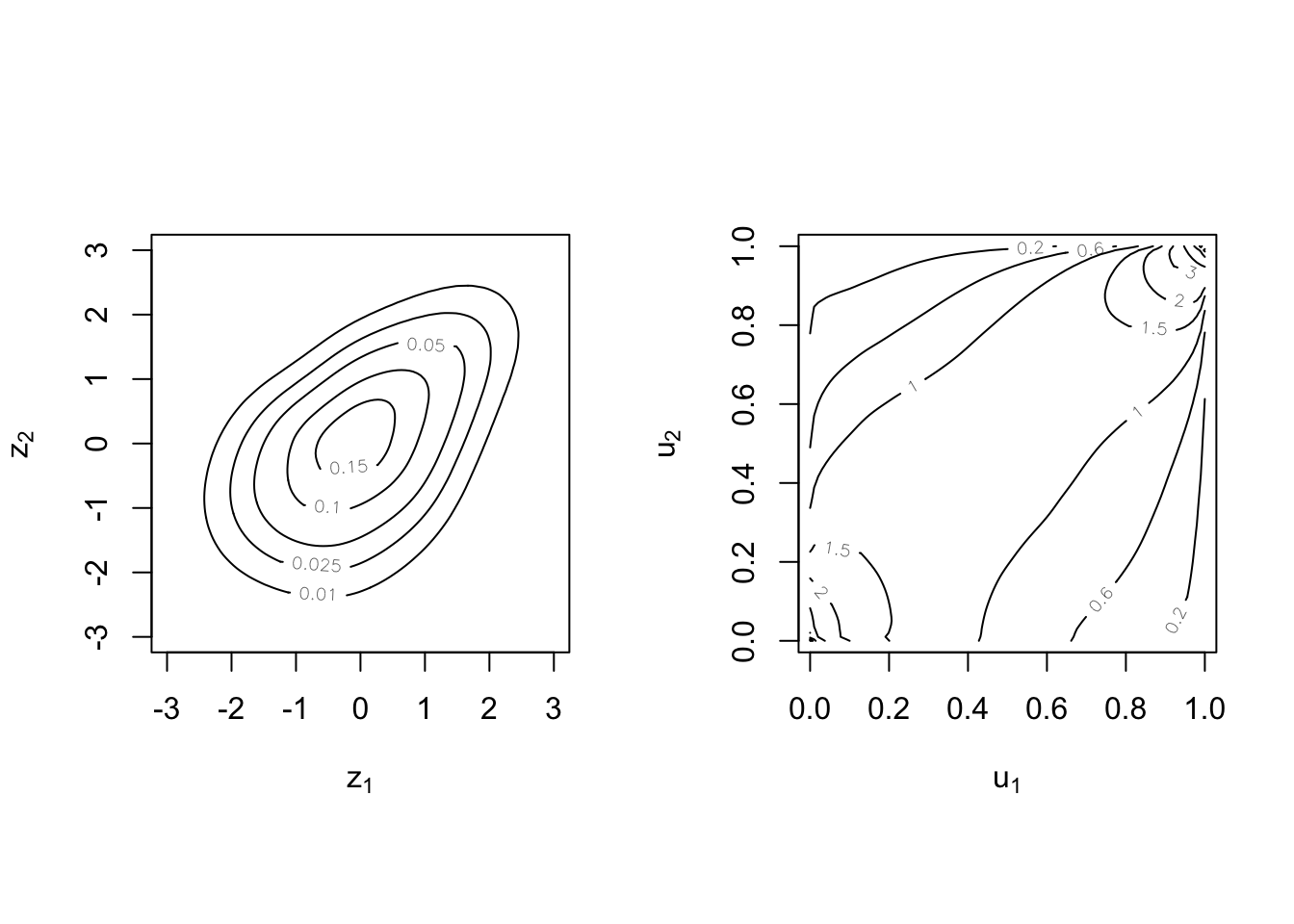
par(mfrow = c(1, 2), pty = "s")
BiCopKDE(pobs(log(Loss.ALAE$LOSS)), pobs(log(Loss.ALAE$ALAE)))
BiCopKDE(pobs(log(Loss.ALAE$LOSS)), pobs(log(Loss.ALAE$ALAE)),
margins = "unif")
- Case 1: loss variable is not censored, i.e.
where
- Case 2: loss variable is censored, i.e.
where
- Pareto marginals:
- For the copulas, several candidates were used:
-
Akaike Information Criterion (AIC)
-
In the absence of a better way to choosing/selecting a copula model, one may use the AIC criterion defined by
-
Lower AIC generally is preferred.
To find the distribution of the sum of dependent random variables with copulas (one approach):
- Fit marginals independently
- Describe/fit dependence with a copula (roughly)
- Get a sense of data (scatterplots, dependence measures)
- Choose candidate copulas
- For each candidate, estimate parameters via MLE
- Choose a copula based on nll(highest) or AIC(lowest)
- If focusing on the sum, one might do simulations to look at the distributions of aggregates, and how they compare with the original data.
Coefficients of tail dependence #
Motivation #
- In insurance and investment applications it is the large outcomes (losses) that particularly tend to occur together, whereas small claims tend to be fairly independent
- This is one of the reasons why tails (especially right tails) tend to be fatter in financial applications.
- A good understanding of tail behaviour is hence very important.
- It is possible to derive tail properties due to dependence from a copula model.
- The indicator we are considering here is the coefficient of tail dependence.
- Tail dependence can take values between 0 (no dependence) and 1 (full dependence).
VineCopula::BiCopPar2TailDepcomputes the theoretical tail dependence coefficients for copulas of theBiCopfamily.
Coefficient of lower tail dependence #
The coefficient of lower tail dependence is defined as
The lower tail of the Clayton copula is comprehensive in that
it allows for tail coefficients of 0 (as
Coefficient of upper tail dependence #
The coefficient of upper tail dependence is defined similarly but using the survival copula, which yields
Note
References #
Avanzi, Benjamin, Luke C. Cassar, and Bernard Wong. 2011. “Modelling Dependence in Insurance Claims Processes with Lévy Copulas.” ASTIN Bulletin 41 (2): 575–609.
Kurowicka, D., and H. Joe. 2011. Dependence Modeling Vine Copula Handbook.
Nelsen, R. B. 1999. An Introduction to Copulas. Springer.
Sklar, A. 1959. “Fonctions de Répartition à $n$ Dimensions Et Leurs Marges.” Publications de l’Institut de Statistique de l’Université de Paris 8: 229–31.
Vigen, Tyler. 2015. “Spurious Correlations (Last Accessed on 18 March 2015 on http://www.tylervigen.com).”
Wikipedia. 2020. “Copula: Probability Theory.” https://www.wikiwand.com/en/Copula_(probability_theory).

